
如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
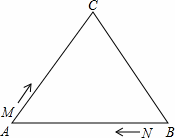
解:(1)设点M、N运动x秒后,M、N两点重合,
x×1+12=2x,解得:x=12;
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB-BN=12-2t,∵三角形△AMN是等边三角形,∴t=12-2t,
解得t=4,∴点M、N运动4秒后,可得到等边三角形△AMN.

(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,∴AN=AM,∴∠AMN=∠ANM,
∴∠AMC=∠ANB,∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,
在△ACM和△ABN中,
∵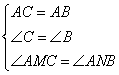 ,∴△ACM≌△ABN,∴CM=BN,
,∴△ACM≌△ABN,∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y-12,NB=36-2y,CM=NB,y-12=36-2y,解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若要求总利润不低于17560元,有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
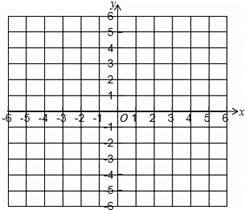
已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
(2015•漳州)国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
| 类别 | 彩电 | 冰箱 | 洗衣机 |
| 进价(元/台) | 2000 | 1600 | 1000 |
| 售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com