
如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,则∠ACB的度数为 .
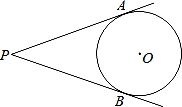
70°或110° .
【考点】切线的性质.
【分析】首先连接OA、OB,在AB弧上任取一点C,连接AC、BC,由PA、PB是⊙O的切线,根据切线的性质,可得∠OAP=∠OBP=90°,又由∠APB=40°,即可求得∠AOB的度数,然后分别从①若C点在优弧AB上与②若C点在劣弧AB上去分析,即可求得∠ACB的度数.
【解答】解:连接OA、OB,在AB弧上任取一点C,连接AC、BC,
∵PA、PB是⊙O的切线,A、B为切点,
∴∠OAP=∠OBP=90°,
∵∠APB=40°,
∴在四边形OAPB中,∠AOB=360°﹣∠APB﹣∠OAP﹣∠OBP=140°.
①若C点在优弧AB上,则∠ACB=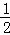 ∠AOB=70°;
∠AOB=70°;
②若C点在劣弧AB上,则∠ACB=180°﹣70°=110°,
故答案为:70°或110°.
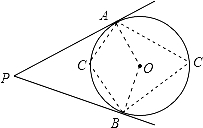
【点评】此题主要考查了切线的性质与圆周角的性质,解题的关键是注意数形结合思想与分类讨论思想的应用,注意辅助线的作法.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
对于抛物线y=﹣ (x+1)2+3,下列结论不正确的是( )
(x+1)2+3,下列结论不正确的是( )
A.抛物线的开口向下
B.对称轴为直线x=1
C.顶点坐标为(﹣1,3)
D.此抛物线是由y=﹣ x2+3向左平移1个单位得到的
x2+3向左平移1个单位得到的
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件;
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
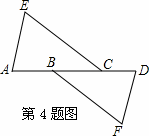
如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的……( )
A.AB=CD; B.EC=BF; C.∠A=∠D; D.AB=BC;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
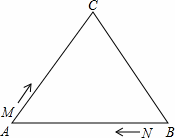
如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com