
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件;
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
【考点】一元二次方程的应用.
【专题】销售问题.
【分析】此题属于经营问题,若设每件衬衫应降价x元,则每件所得利润为(40﹣x)元,但每天多售出2x件即售出件数为(20+2x)件,因此每天赢利为(40﹣x)(20+2x)元,进而可根据题意列出方程求解.
【解答】解:(1)设每件衬衫应降价x元,
根据题意得(40﹣x)(20+2x)=1200,
整理得2x2﹣60x+400=0
解得x1=20,x2=10.
因为要尽量减少库存,在获利相同的条件下,降价越多,销售越快,
故每件衬衫应降20元.
答:每件衬衫应降价20元.
(2)设商场平均每天赢利y元,则
y=(20+2x)(40﹣x)
=﹣2x2+60x+800
=﹣2(x2﹣30x﹣400)=﹣2[(x﹣15)2﹣625]
=﹣2(x﹣15)2+1250.
∴当x=15时,y取最大值,最大值为1250.
答:每件衬衫降价15元时,商场平均每天赢利最多,最大利润为1250元.
【点评】(1)当降价20元和10元时,每天都赢利1200元,但降价10元不满足“尽量减少库存”,所以做题时应认真审题,不能漏掉任何一个条件;
(2)要用配方法将代数式变形,转化为一个完全平方式与一个常数和或差的形式.


科目:初中数学 来源: 题型:
王刚同学在解关于x的方程x2﹣3x+c=0时,误将﹣3x看作+3x,结果解得x1=1,x2=﹣4,则原方程的解为( )
A.x1=﹣1,x2=﹣4 B.x1=1,x2=4 C.x1=﹣1,x2=4 D.x1=2,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)sin2A1+sin2B1= ;sin2A2+sin2B2= ;sin2A3+sin2B3= .猜想:在Rt△ABC中, ∠C=90°,都有sin2A+sin2B= .
∠C=90°,都有sin2A+sin2B= .
(2)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,利用锐角三角比的定义和勾股定理,证明你的猜想.
(3)已知:∠A+∠B=90°,且sinA=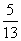 求sinB.
求sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是………………………………………………………………( )
A.8; B.9; C.10; D.11;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
(2015•宜昌模拟)如图,在△ABC中,∠ACB=90°,∠B=30°,CD,CE分别是AB边上的中线和高.
 (1)求证:AE=ED;
(1)求证:AE=ED;
(2)若AC=2,求△CDE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com