
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




科目:初中数学 来源: 题型:
【题目】如图1是2019年11月的日历,用如图2所示的曲尺形框框(有三个方向,从左往右依次记为一、二、三个框) ,可以框住日历中的三个数,设被框住的三个数中最大的数为![]()
日 | 一 | 二 | 三 | 四 | 五 | 六 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

![]() 请用含
请用含![]() 的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
![]() 这三个框分别框住的中间的数之和能恰好是
这三个框分别框住的中间的数之和能恰好是![]() 的倍数吗?如能请求出
的倍数吗?如能请求出![]() 的值,若不能请说明理由.
的值,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
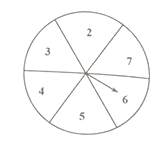
求:(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是 .
②这三条线段能构成等腰三角形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为_________.
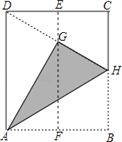
查看答案和解析>>
科目:初中数学 来源: 题型:
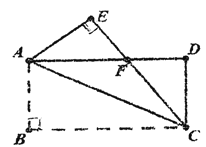
【题目】如图,AC是矩形ABCD的一条对角线,沿AC折叠使点B落在点E处。
(1)求证△AEF≌△CDF.
(2)若AB=4,BC=8,求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, BM切⊙O于点B,点P是⊙O上的一个动点(不经过A,B两点),过O作OQ∥AP交![]() 于点Q,过点P作
于点Q,过点P作![]() 于C,交
于C,交![]() 的延长线于点E,连结
的延长线于点E,连结![]() .
.
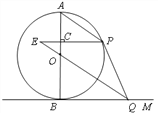
(1)求证:PQ与⊙O相切;
(2)若直径AB的长为12,PC=2EC,求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多![]() ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少![]() ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多![]() ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少![]() ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( )
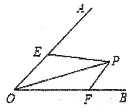
A. 30°B. 45°C. 60°D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国七十周年,南岗区准备对某道路工程进行改造,若请甲工程队单独做此工程需4个月完成,若请乙工程队单独做此工程需6个月完成,若甲、乙两队合作2个月后,甲工程队到期撤离,则乙工程队再单独需几个月能完成?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com