练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】综合题化简及计算
    （1）化简： ﹣
    （2）关于x的一元二次方程kx2﹣2x+3=0有两个不相等的实数根．求：k的取值范围．

    【答案】
    （1）解：原式= +

    =

    =


    （2）解：根据题意得k≠0且△=（﹣2）2﹣4k3＞0，

    解得k＜ 且k≠0


    【解析】（1）分式化简的基本方法有通分、约分，分子分母出现多项式时看能否分解因式，便于约分；（2）一元二次方程有两个不相等实数根的条件包括k0,>0.
    【考点精析】根据题目的已知条件，利用分式的加减法和求根公式的相关知识可以得到问题的答案，需要掌握分式的加减法分为同分母的加减法和异分母的加减法．而异分母的加减法是通过"通分"转化为同分母的加减法进行运算的；根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，完成相应任务：

    折纸三等分角
    三等分角问题（trisection of an angle）是二千四百年前，古希腊人提出的几何三大作图问题之一（三等分任意角、化圆为方、倍立方），即用圆规与直尺（没有刻度，只能做直线的尺子）把一任意角三等分，这问题曾吸引着许多人去研究，但无一成功．1837年法国数学家凡齐尔（1814～1848）运用代数方法证明了，仅用尺规不可鞥呢三等分角．
    如果作图工具没有限制，将条件放宽，将任意角三等分是可以解决的．下面介绍一种折纸三等分任意锐角的方法：
    ①在正方形纸片上折出任意∠SBC，将正方形ABCD对折，折痕为记为MN，再将矩形MBCN对折，折痕记为EF，得到图1；
    ②翻折左下角使点B与EF上的点T重合，点M与SB上的点P重合，点E对折后的对应点记为Q，折痕为记为GH，得到图2；
    ③折出射线BQ，BT，得到图3，则射线BQ，BT就是∠SBC的三等分线．

    下面是证明BQ，BT是∠SBC三等分线的部分过程：
    证明：过T作TK⊥BC，垂足为K，则四边形EBKT为矩形
    根据折叠，得EB=QT，∠EBT=∠QTB，BT=TB
    ∴△EBT≌△QTB，
    ∴∠BQT=∠TEB=90°，
    ∴BQ⊥PT
    …

    学习任务：
    （1）将剩余部分的证明过程补充完整；
    （2）若将图1中的点S与点D重合，重复材料中的操作过程得到图4，请利用图4，直接写出tan15°=（不必化简）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，DB∥AC，且DB=AC，E是AC的中点，

    （1）求证：BC=DE；

    （2）连接AD、BE，若要使四边形DBEA是矩形，则给△ABC添加什么条件，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了保护环境，某化工厂一期工程完成后购买了台甲型和台乙型污水处理设备，共花费资金万元，且每台乙型设备的价格是每台甲型设备价格的，实际运行中发现，每台甲型设备每月能处理污水吨，每台乙型设备每月能处理污水吨．今年该厂二期工程即将完成产生的污水将大大增加，于是该厂决定再购买甲、乙两种型号设备共台用于二期工程的污水处理，预算本次购买资金不超过万元，预计二期工程完成后每月将产生不少于吨污水．

    （1）请你计算每台甲型设备和每台乙型设备的价格各是多少元；

    （2）请你求出用于二期工程的污水处理设备的所有购买方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数y= 与y=﹣kx2+k（k≠0）在同一直角坐标系中的图象可能是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．

    （1）已知点M，N是线段AB的勾股分割点，若AM=2，MN=3，则BN=；
    （2）如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC＞DE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点；

    （3）如图3，已知点M，N是线段AB的勾股分割点，MN＞AM≥BN，四边形AMDC，四边形MNFE和四边形NBHG均是正方形，点P在边EF上，试探究S△ACN ， S△APB ， S△MBH的数量关系．
    S△ACN=；S△MBH=；S△APB=；
    S△ACN ， S△APB ， S△MBH的数量关系是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在创建文明城区的活动中，有两端长度相等的彩色道砖铺设任务，分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度（米）与施工时间（时）之间的关系的部分图像.请解答下列问题.

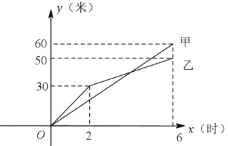
    （1）甲队在的时段内的速度是 米/时.乙队在的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米，乙队铺设彩色道砖的长度是 米.

    （2）如果铺设的彩色道砖的总长度为150米，开挖6小时后，甲队、乙队均增加人手，提高了工作效率，此后乙队平均每小时比甲队多铺5米，结果乙反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数 y1＝k1x与的图象都经过点（2，2）．

    （1）填空：k1＝　 　，k2＝　 　；

    （2）在同一坐标系中作出这两个函数的图象；

    （3）直接写出当y1＞y2时，自变量x的取值范围：　 　．

    查看答案和解析>>

    同步练习册答案