
【题目】阅读下列材料,完成相应任务:
折纸三等分角 |
学习任务:
(1)将剩余部分的证明过程补充完整;
(2)若将图1中的点S与点D重合,重复材料中的操作过程得到图4,请利用图4,直接写出tan15°=(不必化简)
【答案】
(1)解:剩余的证明过程如下:
∵ME=PQ,EB=QT,ME=EB,
∴PQ=QT,
∴BP=BT,
∴∠PBQ=∠TBQ,
∵TK=BE,
∴TK=TQ,
∴∠QBT=∠TBC,
∴射线BQ,BT是∠SBC的三等分线
(2)2﹣ ![]()
【解析】解:(2)同(1)可知:射线BQ,BT是∠DBC的三等分线,
过T作TJ⊥BC,垂足为J,如图所示:
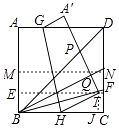
则∠TBJ= ![]() ∠DBC,
∠DBC,
∵四边形ABCD为正方形,
∴∠DBC=45°,
∴∠TBJ=15°,
由折叠性质得:BH=HT,
∴∠TBJ=∠HTB=15°,
∴∠THJ=30°,
设BC=4,则BE=1,
∵将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,TJ⊥BC,
∴四边形EBJT为矩形,
∴TJ=BE=1,
在Rt△THJ中,∠THJ=30°,
∴HT=2TJ=2,HJ=cot30°TJ= ![]() ×1=
×1= ![]() ,
,
∴BJ=BH+HJ=HT+HJ=2+ ![]() ,tan∠TBJ=
,tan∠TBJ= ![]() =
= ![]() =2﹣
=2﹣ ![]() ,
,
即tan15°=2﹣ ![]() ;
;
所以答案是:2﹣ ![]() .
.
【考点精析】掌握翻折变换(折叠问题)和锐角三角函数的定义是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.


科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.

(1)试说明:∠BFD=∠ABC;
(2)若∠ABC=40°,EG∥AD,EH⊥BE,求∠HEG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们经常利用图形描述问题和分析问题.借助直观的几何图形,把问题变得简明、形象,有助于探索解决问题的思路.
(1)在整式乘法公式的学习中,小明为了解释某一公式,构造了几何图形,如图1所示,先画了边长为a,b的大小两个正方形,再延长小正方形的两边,把大正方形分割为四部分,并分别标记为Ⅰ,Ⅱ,Ⅲ,Ⅳ,然后补出图形Ⅴ.显然图形Ⅴ与图形Ⅳ的面积相等,所以图形Ⅰ,Ⅱ,Ⅴ的面积和与图形Ⅰ,Ⅱ,Ⅳ的面积和相等,从而验证了公式.则小明验证的公式是 ;

(2)计算:(x+a)(x+b)= ;请画图说明这个等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
在数学活动课上,老师给出如下问题,让同学们展开探究活动:
问题情境:
如图(1),在△ABC中,∠ACB=90°,AC=BC=a,点D为AB上一点(0<AD< ![]() AB),将线段CD绕点C逆时针旋转90°,得到的对应线段为CE,过点E作EF∥AB,交BC于点F.请你根据上述条件,提出恰当的数学问题并解答.
AB),将线段CD绕点C逆时针旋转90°,得到的对应线段为CE,过点E作EF∥AB,交BC于点F.请你根据上述条件,提出恰当的数学问题并解答.
解决问题:
下面是学习小组提出的三个问题,请你解答这些问题:
(1)“兴趣”小组提出的问题是:求证:AD=EF.
(2)“实践”小组提出的问题是:如图(2),若将△ACD沿AB的垂直平分线对折,得到△BCG,连接EG,则线段EG与EF有怎样的数量关系?请说明理由.
(3)“奋进”小组在“实践”小组探究的基础上,提出了如下问题:延长EF与AC交于点H,连接HD,FG.求证:四边形DGFH是矩形.
提出问题:
(4)完成上述问题的探究后,老师让同学们结合图(3),提一个与四边形DGFH有关的问题.
“智慧”小组提出的问题是:当AD为何值时,四边形DGFH的面积最大?
请你参照智慧小组的做法,再提出一个与四边形DGFH有关的数学问题(提出问题即可,不要求进行解答,但所提问题必须有效)
你提出的问题是:
查看答案和解析>>
科目:初中数学 来源: 题型:
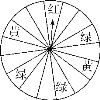
【题目】端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得玩具熊、童话书、水彩笔.小明和妈妈购买了125元的商品,请你回答下列问题:
(1)小明获得奖品的概率是多少?
(2)小明获得玩具熊、童话书、水彩笔的概率分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,对其份数和成绩(十分制)进行整理,制成了如下两幅不完整的统计图.
(1)求本次抽取的作品数量并补全条形统计图;
(2)此次被抽取的作品的平均得分是分.
(3)若该校共征集到800份作品,请估计8分的作品约有多少份?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com