
����Ŀ�����壺��ͼ1����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ�㣮
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��AM=2��MN=3����BN=��
��2����ͼ2���ڡ�ABC�У�FG����λ�ߣ���D��E���߶�BC�Ĺ��ɷָ�㣬��EC��DE��BD������AD��AE�ֱ�FG�ڵ�M��N����֤����M��N���߶�FG�Ĺ��ɷָ�㣻
��3����ͼ3����֪��M��N���߶�AB�Ĺ��ɷָ�㣬MN��AM��BN���ı���AMDC���ı���MNFE���ı���NBHG���������Σ���P�ڱ�EF�ϣ���̽��S��ACN �� S��APB �� S��MBH��������ϵ��
S��ACN=��S��MBH=��S��APB=��
S��ACN �� S��APB �� S��MBH��������ϵ�� �� 
���𰸡�
��1��![]() ��
�� ![]()
��2��֤���ߵ�F��M��N��G�ֱ���AB��AD��AE��AC���ϵ��е㣬
��FM��MN��NG�ֱ��ǡ�ABD����ADE����AEC����λ�ߣ�
��BD=2FM��DE=2MN��EC=2NG��
�ߵ�D��E���߶�BC�Ĺ��ɷָ�㣬��EC��DE��BD��
��EC2=DE2+DB2��
��4NG2=4MN2+4FM2��
��NG2=MN2+FM2��
���M��N���߶�FG�Ĺ��ɷָ��
��3��![]() ?AM2+
?AM2+ ![]() MN?AM,
MN?AM,![]() ?BN2+
?BN2+ ![]() ?MN?BN,
?MN?BN,![]() MN2+
MN2+ ![]() ?MN?AM+
?MN?AM+ ![]() ?MN?BN,S��APB=S��ACN+S��MBH
?MN?BN,S��APB=S��ACN+S��MBH
���������⣺��1�������������
�ٵ�MNΪ����߶�ʱ��
�ߵ� M��N���߶�AB�Ĺ��ɷָ�㣬
��BN= ![]() =
= ![]() =
= ![]() ��
��
�ڵ�BNΪ����߶�ʱ��
�ߵ�M��N���߶�AB�Ĺ��ɷָ�㣬
��BN= ![]() =
= ![]() =
= ![]() ��
��
����������BN�ij�Ϊ ![]() ��
�� ![]() ��
��
�ǡ��ı���AMDC���ı���MNFE���ı���NBHG���������Σ�
��S��ACN= ![]() ��AM+MN��AC=
��AM+MN��AC= ![]() ��AM+MN��AM=
��AM+MN��AM= ![]() AM2+
AM2+ ![]() MNAM��
MNAM��
S��MBH= ![]() ��MN+BN��BH=
��MN+BN��BH= ![]() ��MN+BN��BN=
��MN+BN��BN= ![]() BN2+
BN2+ ![]() MNBN��
MNBN��
S��PAB= ![]() ��AM+NM+BN��FN=
��AM+NM+BN��FN= ![]() ��AM+MN+BN��MN=
��AM+MN+BN��MN= ![]() MN2+
MN2+ ![]() MNAM+
MNAM+ ![]() MNBN��
MNBN��
��S��APB=S��ACN+S��MBH��
���Դ���S��APB=S��ACN+S��MBH��
�����㾫�������ڱ��⿼������������ε����ʣ���Ҫ�˽��Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������β��ܵó���ȷ�𰸣�


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
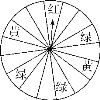
����Ŀ��������ڼ䣬ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת��(ת�̱�ƽ���ֳ�16��)�����涨���˿�ÿ����100Ԫ����Ʒ�����ܻ��һ��תת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ���˿;Ϳ��Էֱ�������ܡ�ͯ���顢ˮ�ʱʣ�С�������蹺����125Ԫ����Ʒ������ش��������⣺
(1)С����ý�Ʒ�ĸ����Ƕ��٣�
(2)С���������ܡ�ͯ���顢ˮ�ʱʵĸ��ʷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��
��



��1����ͼ1��ֱ��д��![]() ��
��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
��2����ͼ2��![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ����ô
����ô![]() ��
��![]() ��������������ϵ����˵�����ɣ�
��������������ϵ����˵�����ɣ�
��3������E��λ����ͼ3��ʾ��![]() ��
��![]() �Էֱ�ƽ��
�Էֱ�ƽ��![]() ��
��![]() ����ֱ��д��
����ֱ��д��![]() ��
��![]() ��������ϵ��
��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⻯����
��1������ ![]() ��
�� ![]()
��2������x��һԪ���η���kx2��2x+3=0����������ȵ�ʵ��������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�ǿѧ���İ�ȫ��ʶ��ijУ��֯��ѧ���μӰ�ȫ֪ʶ���������г�ȡ�˲���ѧ���ɼ����÷���ȡ������������Ϊ100�֣�����ͳ�ƣ�����ͳ��ͼ���£�δ��ɣ�������������⣺


��1����A���Ƶ����B��С24����Ƶ���ֲ�ֱ��ͼ�е�![]() ��
��![]() ��ֵ��
��ֵ��
��2������ͳ��ͼ�У�D�������Ե�Բ�Ľ�Ϊn�㣬��n��ֵ����ȫƵ���ֲ�ֱ��ͼ��
��3�����ɼ���80������Ϊ���㣬ȫУ����2000��ѧ�������Ƴɼ������ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������OABC��������OA��OC�ֱ���y���x���ϣ���֪��A��0��3������C����4��0����
��1�����Ѿ���OABC��ֱ��DE�۵���ʹ��C���ڵ�A����ֱ��DE��OC��AC��AB�Ľ���ֱ�ΪD��F��E�����ۺ�DE�ij���
��2������P��x���ϣ���ƽ�����Ƿ���ڵ�Q��ʹ��P��D��E��QΪ������ı��������Σ������ڣ�����ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2����MΪAC���ϵ�һ���㣬��OA��ȡһ��N��0��1����������OABC�Ƶ�O˳ʱ����תһ�ܣ�����ת�Ĺ����У�M�Ķ�Ӧ��ΪM1����ֱ��д��NM1�����ֵ����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨ����Сѧ�������蹤���У�ijУ�ƻ�����һ�����Ժ͵��Ӱװ壬�����г������֪������![]() ̨���Ժ�
̨���Ժ�![]() ̨���Ӱװ���Ҫ
̨���Ӱװ���Ҫ![]() ��Ԫ������
��Ԫ������![]() ̨���Ժ�
̨���Ժ�![]() ̨���Ӱװ���Ҫ
̨���Ӱװ���Ҫ![]() ��Ԫ��
��Ԫ��
��1����ÿ̨���ԡ�ÿ̨���Ӱװ��������Ԫ��
��2������ѧУʵ�ʣ��蹺�����Ժ͵��Ӱװ干![]() ̨�����ܷ��ò�����
̨�����ܷ��ò�����![]() ��Ԫ�����������Ӱװ����̨��
��Ԫ�����������Ӱװ����̨��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com