
����Ŀ����ͼ1������OABC��������OA��OC�ֱ���y���x���ϣ���֪��A��0��3������C����4��0����
��1�����Ѿ���OABC��ֱ��DE�۵���ʹ��C���ڵ�A����ֱ��DE��OC��AC��AB�Ľ���ֱ�ΪD��F��E�����ۺ�DE�ij���
��2������P��x���ϣ���ƽ�����Ƿ���ڵ�Q��ʹ��P��D��E��QΪ������ı��������Σ������ڣ�����ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2����MΪAC���ϵ�һ���㣬��OA��ȡһ��N��0��1����������OABC�Ƶ�O˳ʱ����תһ�ܣ�����ת�Ĺ����У�M�Ķ�Ӧ��ΪM1����ֱ��д��NM1�����ֵ����Сֵ��

���𰸡���1��![]() ����2����DE�����εĶԽ���ʱ��Q1��0��3������DE�����εı�ʱ��Q2��
����2����DE�����εĶԽ���ʱ��Q1��0��3������DE�����εı�ʱ��Q2��![]() ��3����Q3����
��3����Q3����![]() ��3����Q4����
��3����Q4����![]() ����3������3�����ֵ��5����Сֵ��
����3������3�����ֵ��5����Сֵ��![]() ��
��
��������
��1������DFC�ס�AOC�����DF����֤��EF=DF��
��2�����������ηֱ����ۼ��ɣ���DEΪ���εıߣ���DEΪ���εĶԽ��ߣ�
��3���������M����ͼ3�е�Բ���ڻ�����Բ�ϣ�����ͼ���ɽ�����⣻
�⣺��1���⣺��1�����ı���OABC�Ǿ��Σ�
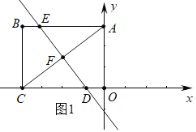
���AOC=90����
��OA=3��OC=4��
��AC=5��
���۵��ɵã�![]()
�ߡ�FCD=��OCA����DFC=��AOC=90����
���DFC�ס�AOC��
![]()
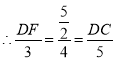
![]()
![]()
���ı���OABC�Ǿ��Σ�
��AB��DC��
���EAF=��DCF
���AFE�ա�CFD��ASA����
��EF=DF��
![]()
���ۺ�DE�ij�Ϊ![]()
��2������ͼ���ɣ�1����֪��![]()

![]()
��DEΪ���εı�ʱ��![]() ���ɵ�
���ɵ�![]() ��
��
��DEΪ���εĶԽ���ʱ��P��C�غϣ�Q��A�غϣ�Q2��0��3����
����Q�ڵ������ޣ�E��Q����x��Գƣ�![]()
�������������������ĵ�Q����Ϊ![]() ��
��![]() ��0��3����
��0��3����![]() ��
��
��3����ͼ3�У���OH��AC����![]()

�۲�ͼ�ο�֪��MN����Сֵ=OM-ON ![]() ��
��
MN�����ֵ=NM��=ON+OM��=1+4=5
![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=x2��4x+2��t��tΪʵ������0��x�� ![]() �ķ�Χ����x���й����㣬��t��ȡֵ��ΧΪ�� ��
�ķ�Χ����x���й����㣬��t��ȡֵ��ΧΪ�� ��
A.��2��t��2
B.��2��t��2
C.�� ![]() ��t��2
��t��2
D.t�ݩ�2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y= ![]() ��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ� ��
��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ1����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ�㣮
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��AM=2��MN=3����BN=��
��2����ͼ2���ڡ�ABC�У�FG����λ�ߣ���D��E���߶�BC�Ĺ��ɷָ�㣬��EC��DE��BD������AD��AE�ֱ�FG�ڵ�M��N����֤����M��N���߶�FG�Ĺ��ɷָ�㣻
��3����ͼ3����֪��M��N���߶�AB�Ĺ��ɷָ�㣬MN��AM��BN���ı���AMDC���ı���MNFE���ı���NBHG���������Σ���P�ڱ�EF�ϣ���̽��S��ACN �� S��APB �� S��MBH��������ϵ��
S��ACN=��S��MBH=��S��APB=��
S��ACN �� S��APB �� S��MBH��������ϵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һˮ���мס��ҡ�������ˮ�ܣ����мס�������Ϊ��ˮ�ܣ��ҹ�Ϊ��ˮ�ܣ���λʱ���ڣ���ˮ���������ˮ������С���ȿ��ס������ܣ�һ��ʱ��ر��ҹܿ����ܣ��־���һ��ʱ�䣬�رռܿ��ҹܣ�������ȷ��ӳˮ����ˮ��y�������ף���ʱ��t��Сʱ���仯��ͼ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ������������Ļ�У������˳�����ȵIJ�ɫ��ש�������ֱ��ס�������ʩ����ͬʱ����ʩ��.��ͼ�Ƿ�ӳ�������ɫ��ש�ij���![]() ���ף���ʩ��ʱ��
���ף���ʩ��ʱ��![]() ��ʱ��֮��Ĺ�ϵ�IJ���ͼ��.������������.
��ʱ��֮��Ĺ�ϵ�IJ���ͼ��.������������.
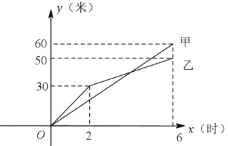
��1������![]() ��ʱ���ڵ��ٶ��� ��/ʱ.�Ҷ���
��ʱ���ڵ��ٶ��� ��/ʱ.�Ҷ���![]() ��ʱ���ڵ��ٶ��� ��/ʱ. 6Сʱ�������ɫ��ש�ij����� �ף��Ҷ������ɫ��ש�ij����� ��.
��ʱ���ڵ��ٶ��� ��/ʱ. 6Сʱ�������ɫ��ש�ij����� �ף��Ҷ������ɫ��ש�ij����� ��.
��2���������IJ�ɫ��ש���ܳ���Ϊ150�ף�����6Сʱ�ӡ��ҶӾ��������֣�����˹���Ч�ʣ��˺��Ҷ�ƽ��ÿСʱ�ȼӶ���5�ף�����ҷ����ȼ���ǰ1Сʱ�������������.����߹���Ч�ʺ�ӡ��Ҷ�ÿСʱ����ij��ȷֱ�Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=��x+4�뷴��������y= ![]() ��ͼ���ཻ�ڵ�A����2��a����������x���ཻ�ڵ�B��
��ͼ���ཻ�ڵ�A����2��a����������x���ཻ�ڵ�B��
��1�����������ı���ʽ��
��2�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=ax+b��a��0����ͼ���뷴��������y= ![]() ��k��0����ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH=3��tan��AOH=
��k��0����ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH=3��tan��AOH= ![]() ����B������Ϊ��m����2����
����B��������m����2����
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����AOC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ����
����![]() �����߶�
�����߶�![]() ������ƽ��2����λ��������ƽ��1����λ��õ��߶�
������ƽ��2����λ��������ƽ��1����λ��õ��߶�![]() ��������
��������![]() ��
��

��1���������![]() �͵�
�͵�![]() �����ꣻ
�����ꣻ
��2����![]() ��
��![]() ���������ÿ��1����λ���ٶ�����ƽ���˶������˶�ʱ��Ϊ
���������ÿ��1����λ���ٶ�����ƽ���˶������˶�ʱ��Ϊ![]() �룬�ʣ��Ƿ����������
�룬�ʣ��Ƿ����������![]() ��ʹ���ı���
��ʹ���ı���![]() ���������8�������ڣ������
���������8�������ڣ������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��3���ڣ�2���������£���![]() ��
��![]() �������ͬʱ����
�������ͬʱ����![]() �ӵ�
�ӵ�![]() ��������ÿ��2����λ���ٶ�����ƽ���˶���������
��������ÿ��2����λ���ٶ�����ƽ���˶���������![]() ��
��![]() ���ڵ�
���ڵ�![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() �룬�ʣ�
�룬�ʣ�![]() ��ֵ�Ƿ�ᷢ���仯�������䣬���������ֵ�����仯����˵�����ɣ�
��ֵ�Ƿ�ᷢ���仯�������䣬���������ֵ�����仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com