
【题目】若抛物线y=x2﹣4x+2﹣t(t为实数)在0<x< ![]() 的范围内与x轴有公共点,则t的取值范围为( )
的范围内与x轴有公共点,则t的取值范围为( )
A.﹣2<t<2
B.﹣2≤t<2
C.﹣ ![]() <t<2
<t<2
D.t≥﹣2
【答案】B
【解析】解:y=x2﹣4x+2﹣t=(x﹣2)2﹣2﹣t,
抛物线的顶点为(2,﹣2﹣t),
当抛物线与x轴的公共点为顶点时,﹣2﹣t=0,解得t=﹣2,
当抛物线在0<x< ![]() 的范围内与x轴有公共点,
的范围内与x轴有公共点,
如图,

﹣t﹣2![]() 0,解得t>﹣2,则x=0时,y>0,即2﹣t>0,解得t<2;
0,解得t>﹣2,则x=0时,y>0,即2﹣t>0,解得t<2;
当x= ![]() 时,y>0,即﹣
时,y>0,即﹣ ![]() ﹣t>0,解得t<﹣
﹣t>0,解得t<﹣ ![]() ,此时t的范围为t<﹣
,此时t的范围为t<﹣ ![]() ,
,
综上所述,t的范围为﹣2≤t<2.
所以答案是:B.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】为增强学生的爱国意识,某中学举办“爱我中华”朗诵比赛,全校学生都参加,并对表现优异的学生进行表彰,设置一、二、三等奖和进步奖共四个奖项,赛后,校统计小组随机抽取了九年级两个班级,并将这两个班的获奖情况绘制成以下两幅不完整的统计图.
请根据图中的信息,解答下列问题:
(1)求本次调查抽取的学生人数,并补全条形统计图;
(2)在扇形统计图中,表示“三等奖”的扇形所对应的圆心角度数是 72 °.
(3)若该校共有2600名学生,试估计得奖的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们经常利用图形描述问题和分析问题.借助直观的几何图形,把问题变得简明、形象,有助于探索解决问题的思路.
(1)在整式乘法公式的学习中,小明为了解释某一公式,构造了几何图形,如图1所示,先画了边长为a,b的大小两个正方形,再延长小正方形的两边,把大正方形分割为四部分,并分别标记为Ⅰ,Ⅱ,Ⅲ,Ⅳ,然后补出图形Ⅴ.显然图形Ⅴ与图形Ⅳ的面积相等,所以图形Ⅰ,Ⅱ,Ⅴ的面积和与图形Ⅰ,Ⅱ,Ⅳ的面积和相等,从而验证了公式.则小明验证的公式是 ;

(2)计算:(x+a)(x+b)= ;请画图说明这个等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
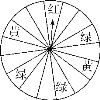
【题目】端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得玩具熊、童话书、水彩笔.小明和妈妈购买了125元的商品,请你回答下列问题:
(1)小明获得奖品的概率是多少?
(2)小明获得玩具熊、童话书、水彩笔的概率分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某造纸企业为了更好地处理污水问题,决定购买10台新型污水处理设备.甲、乙两种型号的设备可选,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/) | 10 | 8 |
处理污水量(吨/月) | 180 | 150 |
(1)经预算:该企业购买污水处理设备的资金不超过85万元,你认为该企业有哪几种购买方案.
(2)在(1)的条件下,若每月需要处理的污水不低于1530吨,为了节约资金,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,对其份数和成绩(十分制)进行整理,制成了如下两幅不完整的统计图.
(1)求本次抽取的作品数量并补全条形统计图;
(2)此次被抽取的作品的平均得分是分.
(3)若该校共征集到800份作品,请估计8分的作品约有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() .
.



(1)如图1,直接写出![]() ,
,![]() 和
和![]() 之间的数量关系.
之间的数量关系.
(2)如图2,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
(3)若点E的位置如图3所示,![]() ,
,![]() 仍分别平分
仍分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点A(0,3)、点C(-4,0).
(1)若把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,求折痕DE的长;
(2)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请直接写出点Q的坐标;若不存在,请说明理由;
(3)如图2,若M为AC边上的一动点,在OA上取一点N(0,1),将矩形OABC绕点O顺时针旋转一周,在旋转的过程中,M的对应点为M1,请直接写出NM1的最大值和最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com