Question

【题目】为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分学生成绩（得分数取正整数，满分为100分）进行统计，绘制统计图如下（未完成），解答下列问题：

（1）若A组的频数比B组小24，求频数分布直方图中的、的值；

（2）扇形统计图中，D部分所对的圆心角为n°，求n的值并补全频数分布直方图；

（3）若成绩在80分以上为优秀，全校共有2000名学生，估计成绩优异的学生有多少名？

Answer 1

【答案】（1）a=16 b=40；（2）126°，图详见解析；（3）940名

【解析】

（1）根据若A组的频数比B组小24，且已知两个组的百分比，据此即可求得总人数，然后根据百分比的意义求得a、b的值；
（2）利用360°乘以对应的比例即可求解；
（3）利用总人数乘以对应的百分比即可求解．

（1）学生总数是24÷（20%-8%）=200（人），
则a=200×8%=16，b=200×20%=40；
（2）n=360×=126°．
C组的人数是：200×25%=50．如图所示：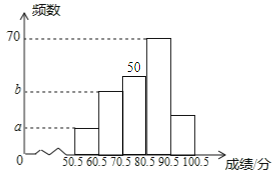
；
（3）样本D、E两组的百分数的和为1-25%-20%-8%=47%，
∴2000×47%=940（名）
答:估计成绩优秀的学生有940名．