
【题目】在南通市中小学标准化建设工程中,某校计划购进一批电脑和电子白板,经过市场考察得知,购买![]() 台电脑和
台电脑和![]() 台电子白板需要
台电子白板需要![]() 万元,购买
万元,购买![]() 台电脑和
台电脑和![]() 台电子白板需要
台电子白板需要![]() 万元.
万元.
(1)求每台电脑、每台电子白板各多少万元;
(2)根据学校实际,需购进电脑和电子白板共![]() 台,若总费用不超过
台,若总费用不超过![]() 万元,则至多购买电子白板多少台?
万元,则至多购买电子白板多少台?
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,则BN=;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
(3)如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,四边形AMDC,四边形MNFE和四边形NBHG均是正方形,点P在边EF上,试探究S△ACN , S△APB , S△MBH的数量关系.
S△ACN=;S△MBH=;S△APB=;
S△ACN , S△APB , S△MBH的数量关系是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建文明城区的活动中,有两端长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度![]() (米)与施工时间
(米)与施工时间![]() (时)之间的关系的部分图像.请解答下列问题.
(时)之间的关系的部分图像.请解答下列问题.
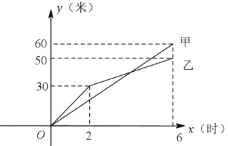
(1)甲队在![]() 的时段内的速度是 米/时.乙队在
的时段内的速度是 米/时.乙队在![]() 的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
(2)如果铺设的彩色道砖的总长度为150米,开挖6小时后,甲队、乙队均增加人手,提高了工作效率,此后乙队平均每小时比甲队多铺5米,结果乙反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与反比例函数y= ![]() 的图象相交于点A(﹣2,a),并且与x轴相交于点B.
的图象相交于点A(﹣2,a),并且与x轴相交于点B.
(1)求反比例函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将30°、45°、60°的三角函数值填入表中,则从表中任意取一个值,是 ![]() 的概率为( )
的概率为( )
α | 30° | 45° | 60° |
sinα | |||
cosα | |||
tanα |
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).
(1)求该反比例函数和一次函数的解析式.
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数 y1=k1x与![]() 的图象都经过点(2,2).
的图象都经过点(2,2).
(1)填空:k1= ,k2= ;
(2)在同一坐标系中作出这两个函数的图象;
(3)直接写出当y1>y2时,自变量x的取值范围: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com