

分析 (1)证明△ADG≌△CDE,可得:AG=CE,根据直接三角形形斜边的中线等于斜边的一半,进而可得:DM=MG=$\frac{1}{2}$AG=$\frac{1}{2}$CE;
(2)延长DM至点N,使MN=DM,连接AN,构造△AMN≌△GMD,证明AN∥GD,利用平行线的性质证明∠NAD=∠CDE;再证明△ADN≌△DCE,进而可证得结论.
解答 解:(1)∵四边形ABCD和四边形DEFG均为正方形,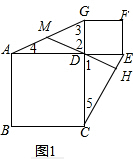
∴AD=CD,DG=DE,∠ADG=∠CDE=90°,
∴△ADG≌△CDE(SAS),
∴AG=CE,∠5=∠4,
∵M是AG的中点,
∴DM=MG=$\frac{1}{2}$AG=$\frac{1}{2}$CE,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∵∠3+∠4=90°,∠5=∠4,
∴∠1+∠5=90°,即DM⊥CE.
故答案为:DM=$\frac{1}{2}$CE,DM⊥CE.
(2)(1)中的结论仍然成立,理由如下:
延长DM至点N,使MN=DM,连接AN,延长MD交CE于点H.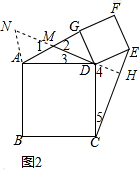
∵M是AG的中点,
∴AM=GM,
又∵∠1=∠2,
∴△AMN≌△GMD(SAS),
∴AN=DG,∠3=∠N,
∴AN∥DG,
∴∠NAD+∠ADG=180°.
∵∠GDE=90°,∠ADC=90°,
∴∠CDE+∠ADG=180°,
∴∠NAD=∠CDE.
∵DE=DG,AN=DG,
∴DE=AN,
∴△ADN≌△DCE(SAS),
∴DN=EC,
∴DM=$\frac{1}{2}$EC.
由△ADN≌△DCE,可得:∠5=∠3,
∵∠3+∠4=90°,
∴∠5+∠4=90°,
∴DM⊥EC.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.能构造全等三角形是解决第(2)小题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n-m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n-m的值.
如图,在平面直角坐标系xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n-m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n-m的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:| 成绩段 | 频数 | 频率 |
| 160≤x<170 | 5 | 0.1 |
| 170≤x<180 | 10 | a |
| 180≤x<190 | b | 0.14 |
| 190≤x<200 | 16 | c |
| 200≤x<210 | 12 | 0.24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 捐 款 (元) | 5 | 10 | 20 | A | 30 |
| 人 数 | 18 | 20 | B | 4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com