
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象与直线y=2x+1交于点A(1,m).
的图象与直线y=2x+1交于点A(1,m).
(1)求k、m的值;
(2)已知点P(n,0)(n≥1),过点P作平行于y轴的直线,交直线y=2x+1于点B,交函数![]() 的图象于点C.横、纵坐标都是整数的点叫做整点.
的图象于点C.横、纵坐标都是整数的点叫做整点.
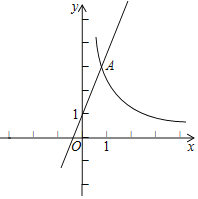
①当n=3时,求线段AB上的整点个数;
②若![]() 的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
【答案】(1)m=3,k=3;(2)①线段AB上有(1,3)、(2,5)、(3,7)共3个整点,②当2≤n<3时,有五个整点.
【解析】
(1)将A点代入直线解析式可求m,再代入![]() ,可求k.
,可求k.
(2)①根据题意先求B,C两点,可得线段AB上的整点的横坐标的范围1≤x≤3,且x为整数,所以x取1,2,3.再代入可求整点,即求出整点个数.
②根据图象可以直接判断2≤n<3.
(1)∵点A(1,m)在y=2x+1上,
∴m=2×1+1=3.
∴A(1,3).
∵点A(1,3)在函数![]() 的图象上,
的图象上,
∴k=3.
(2)①当n=3时,B、C两点的坐标为B(3,7)、C(3,1).
∵整点在线段AB上
∴1≤x≤3且x为整数
∴x=1,2,3
∴当x=1时,y=3,
当x=2时,y=5,
当x=3时,y=7,
∴线段AB上有(1,3)、(2,5)、(3,7)共3个整点.
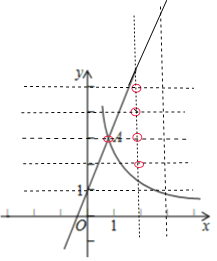
②由图象可得当2≤n<3时,有五个整点.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD、AC、BC于点E、O、F,连接CE和AF.
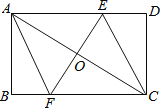
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
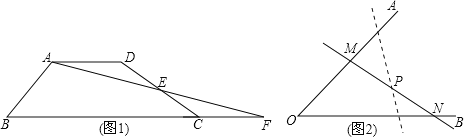
问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
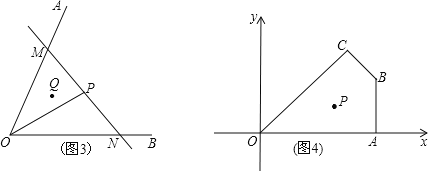
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66,∠POB=30,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66≈0.91,tan66≈2.25,![]() ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、![]() 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于线段MN的“三等分变换”,给出如下定义:如图1,点P,Q为线段MN的三等分点,即MP=PQ=QN,将线段PM以点P为旋转中心顺时针旋转90°得到PM′,将线段QN以点Q为旋转中心顺时针旋转90°得到QN′,则称线段MN进行了三等分变换,其中M′,N′记为点M,N三等分变换后的对应点.
例如:如图2,线段MN,点M的坐标为(1,5),点N的坐标为(1,2),则点P的坐标为(1,4),点Q的坐标为(1,3),那么线段MN三等分变换后,可得:M′的坐标为(2,4),点N′的坐标为(0,3).
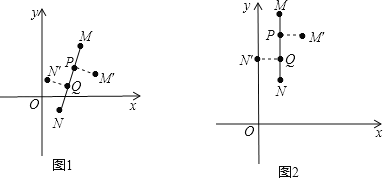
(1)若点P的坐标为(2,0),点Q的坐标为(4,0),直接写出点M′与点N′的坐标;
(2)若点Q的坐标是(0,﹣![]() ),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
(3)若点Q的坐标为(0,0),点M′的坐标为(﹣3,﹣3),直接写出点P与点N的坐标;
(4)点P是以原点O为圆心,1为半径的圆上的一个定点,点P的坐标为(![]() ,
,![]() )当点N′在圆O内部或圆上时,求线段PQ的取值范围及PQ取最大值时点M′的坐标.
)当点N′在圆O内部或圆上时,求线段PQ的取值范围及PQ取最大值时点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据北京市统计局发布的统计数据显示,北京市近五年国民生产总值数据如图1所示,2017年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示,根据以上信息,下列判断错误的是( )
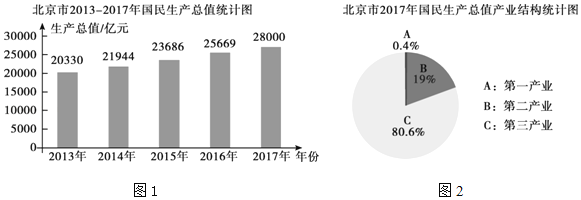
A.2013年至2017年北京市国民生产总值逐年增加
B.2017年第二产业生产总值为5 320亿元
C.2017年比2016年的国民生产总值增加了10%
D.若从2018年开始,每一年的国民生产总值比前一年均增长10%,到2019年的国民生产总值将达到33 880亿元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )
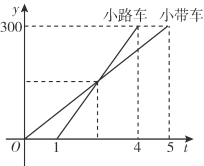
A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中线,
边的中线,![]() 于
于![]() ,连结
,连结![]() ,点
,点![]() 在射线
在射线![]() 上(与
上(与![]() ,
,![]() 不重合)
不重合)
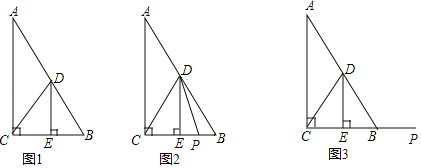
(1)如果![]()
①如图1,![]()
![]()
②如图2,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() ,补全图2猜想
,补全图2猜想![]() 、
、![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(2)如图3,若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,连结
,连结![]() ,将线段
,将线段![]() 绕点逆时针旋转
绕点逆时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,请直接写出
,请直接写出![]() 、
、![]() 、
、![]() 三者的数量关系(不需证明)
三者的数量关系(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后按原路返回:卡车到达甲城比轿车返回甲城早0.5小时,两车到达甲城后均停止行驶,两车距离甲城的路程y(km)与出发时间t(h)之间的关系如图1所示,请结合图象提供的信息解答下列问题:
(1)求轿车和卡车的速度;
(2)求CD段的函数解析式;
(3)若设在行驶过程中,轿车与卡车之间的距离为S(km)行驶的时间为t(h),请你在图2中画出S(km)关于t(h)函数的图象,并标出每段函数图象端点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经纬文教用品商店欲购进A、B两种笔记本,用160元购进的A种笔记本与用240元购进的B种笔记本的数量相同,每本B种笔记本的进价比每本A种笔记本的进价贵10元.
(1)求A、B两种笔记本每本的进价分别为多少元?
(2)若该商店A种笔记本每本售价24元,B种笔记本每本售价35元,准备购进A、B两种笔记本共100本,且这两种笔记本全部售出后总获利高于468元,则最多购进A种笔记本多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com