
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
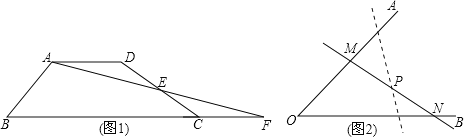
问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
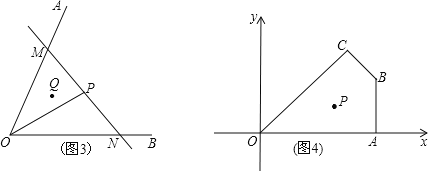
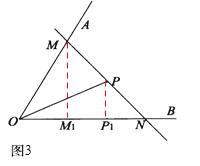
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66,∠POB=30,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66≈0.91,tan66≈2.25,![]() ≈1.73)
≈1.73)
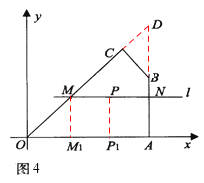
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、![]() 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
【答案】问题情境:根据已知可以求得△ADE≌△FCE,就可以得出S△ADE=S△FCE,从而得出结论。
问题迁移:根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论。
实际运用:∴![]() 。
。
拓展延伸:截得四边形面积的最大值为10
【解析】
问题情境:根据已知可以求得△ADE≌△FCE,就可以得出S△ADE=S△FCE,从而得出结论。
问题迁移:根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论。
实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,再根据条件由三角函数值就可以求出结论。
拓展延伸:分情况讨论当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,由条件可以得出AD=6,就可以求出△OAD的面积,再根据问题迁移的结论就可以求出最大值;
当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,由B、C的坐标可得直线BC的解析式,就可以求出T的坐标,从而求出△OCT的面积,再由问题迁移的结论可以求出最大值,通过比较即可以求出结论。
解:问题情境:证明:∵AD∥BC,∴∠DAE=∠F,∠D=∠FCE。
∵点E为DC边的中点,∴DE=CE。
∵在△ADE和△FCE中,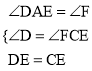 ,
,
∴△ADE≌△FCE(AAS)。∴S△ADE=S△FCE。
∴S四边形ABCE+S△ADE=S四边形ABCE+S△FCE,即S四边形ABCD=S△ABF。
问题迁移:当直线旋转到点P是MN的中点时S△MON最小,理由如下:
如图2,过点P的另一条直线EF交OA、OB于点E、F,
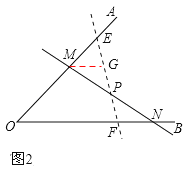
设PF<PE,过点M作MG∥OB交EF于G,
由问题情境可以得出当P是MN的中点时S四边形MOFG=S△MON。
∵S四边形MOFG<S△EOF,∴S△MON<S△EOF。
∴当点P是MN的中点时S△MON最小。
实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,
在Rt△OPP1中,∵∠POB=30°,
∴PP1=![]() OP=2,OP1=2
OP=2,OP1=2![]() 。
。
由问题迁移的结论知,当PM=PN时,△MON的面积最小,
∴MM1=2PP1=4,M1P1=P1N。
在Rt△OMM1中,![]() ,即
,即![]() ,
,
∴![]() 。∴
。∴![]() 。
。
∴![]() 。
。
∴![]() 。
。
拓展延伸:①如图4,当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,
∵C![]() ,∴∠AOC=45°。∴AO=AD。
,∴∠AOC=45°。∴AO=AD。
∵A(6,0),∴OA=6。∴AD=6。
∴![]() 。
。
由问题迁移的结论可知,当PN=PM时,△MND的面积最小,
∴四边形ANMO的面积最大。
作PP1⊥OA,MM1⊥OA,垂足分别为P1,M1,
∴M1P1=P1A=2。∴OM1=M1M=2,∴MN∥OA。
∴![]() 。
。
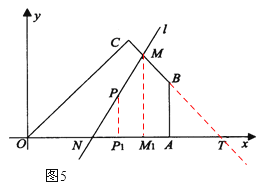
②如图5,当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,
设直线BC的解析式为y=kx+b,
∵C![]() 、B(6,3),
、B(6,3),
∴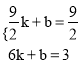 ,解得:
,解得:![]() 。
。
∴直线BC的解析式为![]() 。
。
当y=0时,x=9,∴T(9,0)。
∴![]() 。
。
由问题迁移的结论可知,当PM=PN时,△MNT的面积最小,
∴四边形CMNO的面积最大。
∴NP1=M1P1,MM1=2PP1=4。∴![]() ,解得x=5。∴M(5,4)。
,解得x=5。∴M(5,4)。
∴OM1=5。
∵P(4,2),∴OP1=4。∴P1M1=NP1=1。∴ON=3。∴NT=6。
∴![]() 。
。
∴![]() 。
。
∴综上所述:截得四边形面积的最大值为10。


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
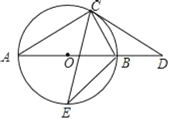
【题目】AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB的延长线相交于点D,CA=CD.
(1)连接BC,求证:BC=OB;
(2)E是![]() 中点,连接CE,BE,若BE=2,求CE的长.
中点,连接CE,BE,若BE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
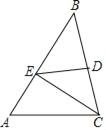
【题目】已知如图,在△ABC中,∠B=45°,点D是BC边的中点,DE⊥BC于点D,交AB于点E,连接CE.
(1)求∠AEC的度数;
(2)请你判断AE、BE、AC三条线段之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
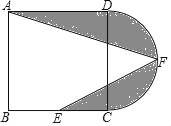
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B的对应点为B',C的对应点为C',MN是折痕若B'M=1,则CN的长为____.
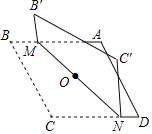
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象与直线y=2x+1交于点A(1,m).
的图象与直线y=2x+1交于点A(1,m).
(1)求k、m的值;
(2)已知点P(n,0)(n≥1),过点P作平行于y轴的直线,交直线y=2x+1于点B,交函数![]() 的图象于点C.横、纵坐标都是整数的点叫做整点.
的图象于点C.横、纵坐标都是整数的点叫做整点.
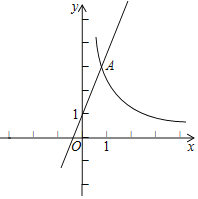
①当n=3时,求线段AB上的整点个数;
②若![]() 的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
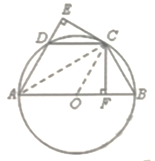
【题目】如图,AB是⊙O的直径,D、D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF.
(1)求证:CE是⊙O的切线;
(2)连接CD、CB,若AD=CD=a,求四边形ABCD面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com