
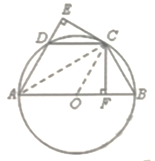
【题目】如图,AB是⊙O的直径,D、D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF.
(1)求证:CE是⊙O的切线;
(2)连接CD、CB,若AD=CD=a,求四边形ABCD面积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接OC,AC,可先证明AC平分∠BAE,结合圆的性质可证明OC∥AE,可得∠OCB=90°,可证得结论;
(2)可先证得四边形AOCD为平行四边形,再证明△OCB为等边三角形,可求得CF、AB,利用梯形的面积公式可求得答案.
(1)证明:连接OC,AC.
∵CF⊥AB,CE⊥AD,且CE=CF.
∴∠CAE=∠CAB.
∵OC=OA,
∴∠CAB=∠OCA.
∴∠CAE=∠OCA.
∴OC∥AE.
∴∠OCE+∠AEC=180°,
∵∠AEC=90°,
∴∠OCE=90°即OC⊥CE,
∵OC是⊙O的半径,点C为半径外端,
∴CE是⊙O的切线.
(2)解:∵AD=CD,
∴∠DAC=∠DCA=∠CAB,
∴DC∥AB,
∵∠CAE=∠OCA,
∴OC∥AD,
∴四边形AOCD是平行四边形,
∴OC=AD=a,AB=2a,
∵∠CAE=∠CAB,
∴CD=CB=a,
∴CB=OC=OB,
∴△OCB是等边三角形,
在Rt△CFB中,CF=![]() ,
,
∴S四边形ABCD=![]() (DC+AB)CF=
(DC+AB)CF=![]()


科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
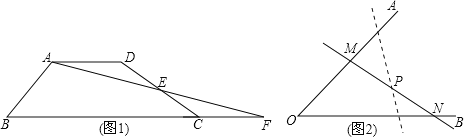
问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
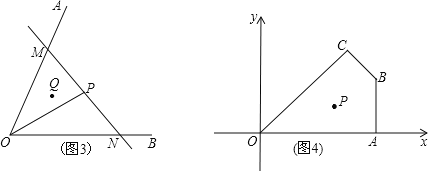
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66,∠POB=30,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66≈0.91,tan66≈2.25,![]() ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、![]() 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中线,
边的中线,![]() 于
于![]() ,连结
,连结![]() ,点
,点![]() 在射线
在射线![]() 上(与
上(与![]() ,
,![]() 不重合)
不重合)
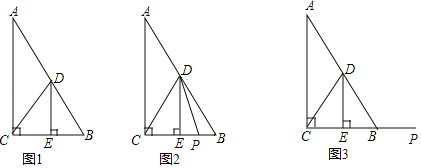
(1)如果![]()
①如图1,![]()
![]()
②如图2,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() ,补全图2猜想
,补全图2猜想![]() 、
、![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(2)如图3,若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,连结
,连结![]() ,将线段
,将线段![]() 绕点逆时针旋转
绕点逆时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,请直接写出
,请直接写出![]() 、
、![]() 、
、![]() 三者的数量关系(不需证明)
三者的数量关系(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
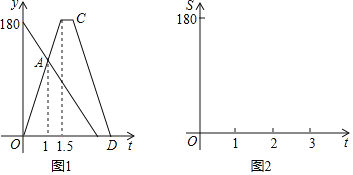
【题目】一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后按原路返回:卡车到达甲城比轿车返回甲城早0.5小时,两车到达甲城后均停止行驶,两车距离甲城的路程y(km)与出发时间t(h)之间的关系如图1所示,请结合图象提供的信息解答下列问题:
(1)求轿车和卡车的速度;
(2)求CD段的函数解析式;
(3)若设在行驶过程中,轿车与卡车之间的距离为S(km)行驶的时间为t(h),请你在图2中画出S(km)关于t(h)函数的图象,并标出每段函数图象端点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验.
在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.

根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
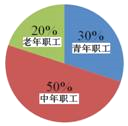
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
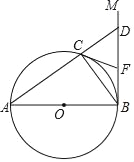
【题目】如图,AB为⊙O的直径,直线BM⊥AB于点B,点C在⊙O上,分别连接BC,AC,且AC的延长线交BM于点D,CF为⊙O的切线交BM于点F.
(1)求证:CF=DF;
(2)连接OF,若AB=10,BC=6,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经纬文教用品商店欲购进A、B两种笔记本,用160元购进的A种笔记本与用240元购进的B种笔记本的数量相同,每本B种笔记本的进价比每本A种笔记本的进价贵10元.
(1)求A、B两种笔记本每本的进价分别为多少元?
(2)若该商店A种笔记本每本售价24元,B种笔记本每本售价35元,准备购进A、B两种笔记本共100本,且这两种笔记本全部售出后总获利高于468元,则最多购进A种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
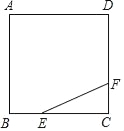
【题目】如图,正方形ABCD的边长为3,点E,F分别在边BCCD上,BE=CF=1,小球P从点E出发沿直线向点F运动,完成第1次与边的碰撞,每当碰到正方形的边时反弹,反弹时反射角等于入射角,则小球P与正方形的边第2次碰撞到__边上,小球P与正方形的边完成第5次碰撞所经过的路程为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com