
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B的对应点为B',C的对应点为C',MN是折痕若B'M=1,则CN的长为____.
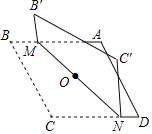
【答案】4.
【解析】
连接AC、BD,利用菱形的性质得OC=![]() AC=3,OD=
AC=3,OD=![]() BD=4,∠COD=90°,再利用勾股定理计算出CD=5,根据△OBM≌△ODN得到DN=BM,然后根据折叠的性质得BM=B'M=1,从而有DN=1,于是计算CD﹣DN即可.
BD=4,∠COD=90°,再利用勾股定理计算出CD=5,根据△OBM≌△ODN得到DN=BM,然后根据折叠的性质得BM=B'M=1,从而有DN=1,于是计算CD﹣DN即可.
连接AC、BD,如图,
∵点O为菱形ABCD的对角线的交点,
∴OC=![]() AC=3,OD=
AC=3,OD=![]() BD=4,∠COD=90°,
BD=4,∠COD=90°,
在Rt△COD中,CD=![]() =5,
=5,
∵AB∥CD,
∴∠MBO=∠NDO,
在△OBM和△ODN中,
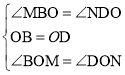 ,
,
∴△OBM≌△ODN(ASA),
∴DN=BM,
∵过点O折叠菱形,使B,B′两点重合,MN是折痕,
∴BM=B'M=1,
∴DN=1,
∴CN=CD﹣DN=5﹣1=4.
故答案为:4.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】研究发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的.讲课开始时,学生的注意力激增,中间有一段时间,学生的注意力保持平稳状态,随后开始分散.学生注意力指标数![]() 随时间
随时间![]() 变化的函数图象如图所示(
变化的函数图象如图所示(![]() 越大表示学生注意力越集中).当
越大表示学生注意力越集中).当![]() 时,图象是抛物线的一部分;当
时,图象是抛物线的一部分;当![]() 和
和![]() 时,图象是线段.根据图象回答问题:
时,图象是线段.根据图象回答问题:
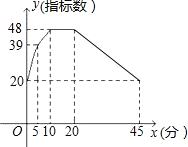
(1)课堂上,学生注意力保持平稳状态的时间段是_______.
(2)结合函数图象回答,一道几何综合题如果需要讲25分钟,老师最好在上课后大约第______分钟到第________分钟讲这道题,能使学生处于注意力比较集中的听课状态.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l是线段MN的垂直平分线,交线段MN于点O,在MN下方的直线l上取一点P,连接PN,以线段PN为边,在PN上方作正方形NPAB,射线MA交直线l于点C,连接BC.
(1)设∠ONP=α,求∠AMN的度数;
(2)写出线段AM、BC之间的等量关系,并证明.
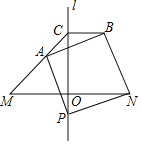
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
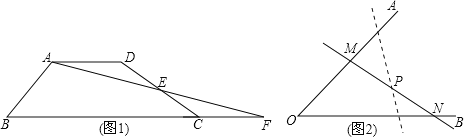
问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
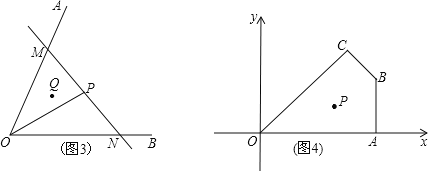
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66,∠POB=30,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66≈0.91,tan66≈2.25,![]() ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、![]() 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx﹣3与双曲线![]() 的两个交点为A,B,其中A(﹣1,m).
的两个交点为A,B,其中A(﹣1,m).
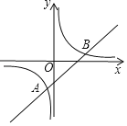
(1)求m的值及直线的表达式;
(2)若点M为x轴上一个动点,且△AMB为直角三角形,直接写出满足条件的点M的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于线段MN的“三等分变换”,给出如下定义:如图1,点P,Q为线段MN的三等分点,即MP=PQ=QN,将线段PM以点P为旋转中心顺时针旋转90°得到PM′,将线段QN以点Q为旋转中心顺时针旋转90°得到QN′,则称线段MN进行了三等分变换,其中M′,N′记为点M,N三等分变换后的对应点.
例如:如图2,线段MN,点M的坐标为(1,5),点N的坐标为(1,2),则点P的坐标为(1,4),点Q的坐标为(1,3),那么线段MN三等分变换后,可得:M′的坐标为(2,4),点N′的坐标为(0,3).
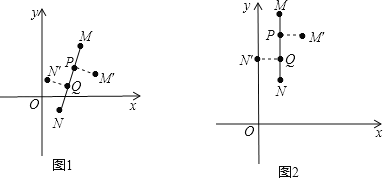
(1)若点P的坐标为(2,0),点Q的坐标为(4,0),直接写出点M′与点N′的坐标;
(2)若点Q的坐标是(0,﹣![]() ),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
(3)若点Q的坐标为(0,0),点M′的坐标为(﹣3,﹣3),直接写出点P与点N的坐标;
(4)点P是以原点O为圆心,1为半径的圆上的一个定点,点P的坐标为(![]() ,
,![]() )当点N′在圆O内部或圆上时,求线段PQ的取值范围及PQ取最大值时点M′的坐标.
)当点N′在圆O内部或圆上时,求线段PQ的取值范围及PQ取最大值时点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )
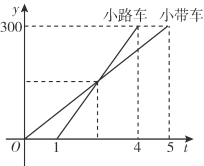
A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
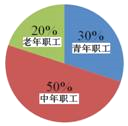
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com