
【题目】如图,在平面直角坐标系xOy中,直线y=kx﹣3与双曲线![]() 的两个交点为A,B,其中A(﹣1,m).
的两个交点为A,B,其中A(﹣1,m).
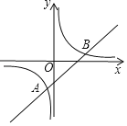
(1)求m的值及直线的表达式;
(2)若点M为x轴上一个动点,且△AMB为直角三角形,直接写出满足条件的点M的个数.
【答案】(1)m=﹣4,y=x﹣3;(2)点M有4个
【解析】
(1)先利用待定系数法求出点A坐标,进而代入双曲线解析式中即可得出结论;
(2)先求出点B的坐标,分三种情况,用勾股定理建立方程即可求出结论.
解:(1)把A(﹣1,m)代入![]() 得
得
∴m=﹣4
把A(﹣1,﹣4)代入y=kx﹣3
∴﹣4=﹣k﹣3
∴k=1
∴y=x﹣3,
(2)由(1)知,直线AB的解析式为y=x﹣3①,
∵双曲线的解析式为![]() ②,
②,
联立①②解得,![]() 或
或![]() ,
,
∴A(﹣1,﹣4),B(4,1),
设点M的坐标为(m,0),
∴AB2=50,AM2=(m+1)2+16,BM2=(m﹣4)2+1
∵△AMB是直角三角形,
∴①当∠AMB=90°时,AM2+BM2=AB2,
∴50=(m+1)2+16+(m﹣4)2+1,
∴![]() ,
,
∴M(![]() ,0)或(
,0)或(![]() ,0);
,0);
②当∠BAM=90°时,AB2+AM2=BM2,
∴50+(m+1)2+16=(m﹣4)2+1,
∴m=﹣5,
∴M(﹣5,0);
③当∠ABM=90°时,AB2+BM2=AM2,
∴50+(m﹣4)2+1=(m+1)2+16,
∴m=5,
∴M(5,0)
∴满足条件的点M有4个.


科目:初中数学 来源: 题型:
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲打字员计划用若干小时完成文稿的电脑输入工作,两小时后,乙打字员协助此项工作,且乙打字员文稿电脑输入的速度是甲的1.5倍,结果提前6小时完成任务,则甲打字员原计划完成此项工作的时间是( )
A.17小时B.14小时C.12小时D.10小时
查看答案和解析>>
科目:初中数学 来源: 题型:
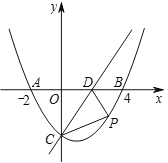
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
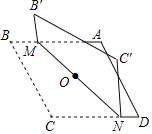
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B的对应点为B',C的对应点为C',MN是折痕若B'M=1,则CN的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1与x轴交于A,B两点(点A在点B左侧)

(1)求抛物线的顶点坐标(用含m的代数式表示);
(2)求线段AB的长;
(3)抛物线与y轴交于点C(点C不与原点O重合),若△OAC的面积始终小于△ABC的面积,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校需要购买A、B两种品牌的篮球,购买A种品牌的篮球30个,B种品牌的篮球20个,共花费5400元,已知购买一个B种品牌的篮球比购买一个A钟品牌的篮球多花20元.
(1)求购买一个A种品牌、一个B种品牌的篮球各需多少元?
(2)学校为了响应习“篮球进校园”的号召,决定再次购进A、B两种品牌球共45个,正好是上商场对商品的促销活动,A品牌篮球售价比第一次购买时降低19元,B品牌篮球按第一次购买时售价的9折出售,如果学校此次购买A、B两种品牌篮球的总费用不超过第一次花费的80%,且保证这次购买的B种品牌篮球不少于15个,则这次学校有几种购买方案?
(3)学校在第二次购买活动中至少需要多少资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且点
两点,且点![]() ,点
,点![]() 在
在![]() 轴正半轴上运动,过点
轴正半轴上运动,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
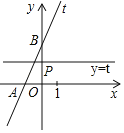
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)当![]() 时,直线
时,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)当![]() 时,若直线
时,若直线![]() 与直线
与直线![]() 和(2)反比例函数的图象分别交于点
和(2)反比例函数的图象分别交于点![]() ,
,![]() ,当
,当![]() 间距离大于等于2时,求
间距离大于等于2时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x1x2+y1y2=0,且A,B均不为原点,则称A和B互为正交点.比如:A(1,1),B(2,﹣2),其中1×2+1×(﹣2)=0,那么A和B互为正交点.
(1)点P和Q互为正交点,P的坐标为(﹣2,3),
①如果Q的坐标为(6,m),那么m的值为多少;
②如果Q的坐标为(x,y),求y与x之间的关系式;
(2)点M和N互为正交点,直接写出∠MON的度数;
(3)点C,D是以(0,2)为圆心,半径为2的圆上的正交点,以线段CD为边,构造正方形CDEF,圆心F在正方形CDEF的外部,求线段OE长度的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com