
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1与x轴交于A,B两点(点A在点B左侧)

(1)求抛物线的顶点坐标(用含m的代数式表示);
(2)求线段AB的长;
(3)抛物线与y轴交于点C(点C不与原点O重合),若△OAC的面积始终小于△ABC的面积,求m的取值范围.
【答案】(1)(m,﹣1);(2)2;(3)﹣1<m<3且 m≠1
【解析】
(1)将抛物线配方成顶点式即可得顶点坐标;
(2)求出y=0时x的值即可得;
(3)由△OAC与△ABC等高且△OAC的面积小于△ABC的面积,知OA<AB,分点A在x轴的正半轴和点A在x轴的负半轴解答可得.
解:(1)y=x2﹣2mx+m2﹣1=(x﹣m)2﹣1,
∴顶点为(m,﹣1);
(2)令y=0
∴x2﹣2mx+m2﹣1=0
解得:x1=m﹣1,x2=m+1,
∵点 A在点B的左侧,
∴A(m﹣1,0),B(m+1,0),
∴AB=(m+1)﹣( m﹣1 )=2;
(3)∵△OAC与△ABC等高
△OAC的面积小于△ABC的面积
∴OA<AB,
①当点A在x轴的正半轴上时,

如图1,
则m﹣1<2,解得:m<3;
②当点A在x轴的负半轴上时,

则1﹣m<2,解得:m>﹣1,
又∵点C不与原点O重合,
∴m 2﹣1≠0,m≠±1,
∴﹣1<m<3且 m≠1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
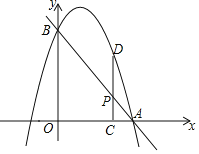
【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC![]()
![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)若抛物线的解析式为![]() ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与![]() AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
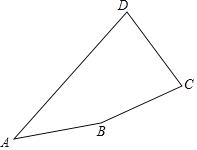
【题目】如图,在凸四边形ABCD中,AB=BC=CD,∠ABC+∠BCD=240°.设∠ABC=α.
(1)利用尺规,以CD为边在四边形内部作等边△CDE.(保留作图痕迹,不需要写作法)
(2)连接AE,判断四边形ABCE的形状,并说明理由.
(3)求证:∠ADC=![]() α;
α;
(4)若CD=6,取CD的中点F,连结AF,当∠ABC等于多少度时,AF最大,最大值为多少.(直接写出答案,不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
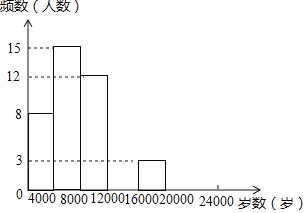
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx﹣3与双曲线![]() 的两个交点为A,B,其中A(﹣1,m).
的两个交点为A,B,其中A(﹣1,m).
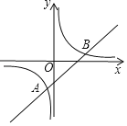
(1)求m的值及直线的表达式;
(2)若点M为x轴上一个动点,且△AMB为直角三角形,直接写出满足条件的点M的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量山坡上的电线杆PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为30°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是60°,求信号塔PQ得高度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).
小强根据他学习函数的经验做了如下的探究.下面是小强的探究过程,请补充完整:
建立函数模型:
设矩形小花园的一边长为x米,篱笆长为y米.则y关于x的函数表达式为________;列表(相关数据保留一位小数):
根据函数的表达式,得到了x与y的几组值,如下表:
x | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y | 17 | 10 | 8.3 | 8.2 | 8.7 | 9.3 | 10.8 | 11.6 |
描点、画函数图象:
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
观察分析、得出结论:
根据以上信息可得,当x=________时,y有最小值.
由此,小强确定篱笆长至少为________米.
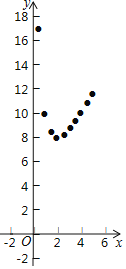
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com