
����Ŀ���ֽ����˶�����Խ��Խ����˹�ע��ϲ����ij��ȤС���������������50����ʦij�ա����˶����еIJ����������ͳ�����������������µ�ͳ��ͼ��������������
���� | Ƶ�� | Ƶ�� |
0��x��4000 | 8 | a |
4000��x��8000 | 15 | 0.3 |
8000��x��12000 | 12 | b |
12000��x��16000 | c | 0.2 |
16000��x��20000 | 3 | 0.06 |
20000��x��24000 | d | 0.04 |
�����������Ϣ������������⣺
��1��д��a��b��c��d��ֵ����ȫƵ���ֲ�ֱ��ͼ��
��2������Լ��37800����ʦ���õ�����������ݹ��������߲�������12000��������12000�����Ľ�ʦ�ж�������
��3������50��������Ľ�ʦ�У�ѡȡ�����߲�������16000��������16000����������ʦ���ҷ����ĵã���ѡȡ��������ʦǡ�ö���20000��������20000�������ϵĸ��ʣ�
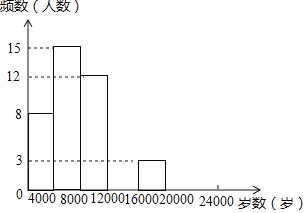
���𰸡���1��a=0.16��b=0.24��c=10��d=2����ȫƵ���ֲ�ֱ��ͼ����������2��11340������3��![]() ��
��
��������
��1������Ƶ��=Ƶ���������ɵô𰸣���2���������г���12000��������12000������Ƶ��֮�ͳ����������ɵô𰸣���3������״ͼ�г����еȿ��ܽ�������ݸ��ʹ�ʽ���ɵã�
��1��a=8��50=0.16��b=12��50=0.24��c=50��0.2=10��d=50��0.04=2��
��ȫƵ���ֲ�ֱ��ͼ���£�
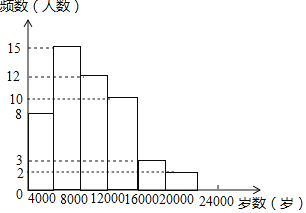
��2��37800����0.2+0.06+0.04��=11340��
�𣺹��������߲�������12000��������12000�����Ľ�ʦ��11340����
��3����16000��x��20000��3����ʦ�ֱ�ΪA��B��C��
20000��x��24000��2����ʦ�ֱ�ΪX��Y��
����״ͼ���£�
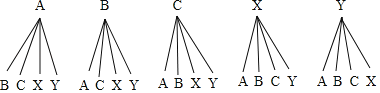
����״ͼ��֪����ѡȡ��������ʦǡ�ö���20000��������20000�������ϵĸ���Ϊ![]() =
=![]() ��
��


 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ�����1������1�������ҿڴ�����1������2��������Щ�����ɫ�����������
��1�����ڴ����������1������ǡ�����������ĸ���Ϊ������ ����
��2���ֱ�Ӽס��������ڴ��и��������1�����������б�����״ͼ�ķ�����������2�����ǰ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ����ҩƷ���ڡ�����Σ�շ����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ�˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������ˣ�
��1������ѡȡ�����ķ����������һ���� ����ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ������ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ������ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
��2�����γ������˷��֣����ܵ��˵ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�����ͼ��

��m= ��n= ��
����ȫ����ͳ��ͼ��
�����ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��
����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
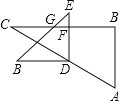
����Ŀ����ͼ��ʾ����ABCΪRt������ACB��90�㣬��DΪAB���е㣬��EΪ��AC�ϵĵ㣬����DE������E��EF��ED��BC��F����DE��EFΪ�ڱ�������DEFG����֪AC��8��
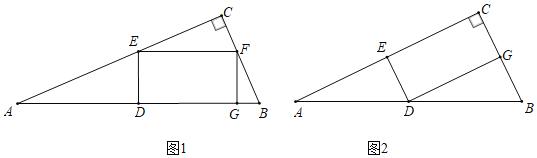
��1����ͼ1��ʾ����BC��6����G�ڱ�AB��ʱ����DE�ij���
��2����ͼ2��ʾ����![]() ����G�ڱ�BC��ʱ����BC�ij���
����G�ڱ�BC��ʱ����BC�ij���
��3������![]() ���ҵ�Gǡ������Rt��ABC�ı��ϣ���BC�ij���
���ҵ�Gǡ������Rt��ABC�ı��ϣ���BC�ij���
����![]() ��nΪ�����������ҵ�Gǡ������Rt��ABC�ı��ϣ���ֱ��д��BC�ij���
��nΪ�����������ҵ�Gǡ������Rt��ABC�ı��ϣ���ֱ��д��BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ABCD�У�E��CD����һ�㣬
��1������ADE�Ƶ�A��˳ʱ�뷽����ת��ʹAD��AB�غϣ��õ���ABF����ͼ1��ʾ���۲��֪����DE��ȵ��߶����� ������AFB=���� ��
��2����ͼ2��������ABCD�У�P��Q�ֱ���BC��CD���ϵĵ㣬�ҡ�PAQ=45������ͨ����ת�ķ�ʽ˵����DQ+BP=PQ��
��3���ڣ�2�����У�����BD�ֱ�AP��AQ��M��N���㻹������ת��˼��˵��BM2+DN2=MN2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y����x2+2x+8��x�ύ��B��C���㣬��Dƽ��BC������x���ϲ��A��Ϊ�������ϵĶ��㣬�ҡ�BACΪ��ǣ���AD��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y=ax2+bx+c��ͼ����x��ֱ���A��B���㣬��y�ύ�ڵ�C����tan��ABC=3��һԪ���η���ax2+bx+c=0������Ϊ��8��2��
��1������κ����Ľ���ʽ��
��2��ֱ��l�Ƶ�A��ABΪ��ʼλ��˳ʱ����ת��ACλ��ֹͣ��l���߶�BC���ڵ�D��P��AD���е㣮
�����P���˶�·�̣�
����ͼ2������D��DE��ֱx���ڵ�E����DF��AC����ֱ���ڵ�F������PE��PF����l�˶������У���EPF�Ĵ�С�Ƿ�ı䣿��˵�����ɣ�
��3���ڣ�2���������£�����EF������PEF�ܳ�����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����x2+bx+c��x�ύ�ڵ�A����1��0����B��3��0������y�ύ�ڵ�C����D��ֱ��BC�Ϸ���������һ���㣮
��1���������ߵĽ���ʽ��
��2����ͼ1������BD��CD�����D�ĺ�����Ϊm����BCD�����Ϊs�������s��m�ĺ�����ϵʽ�������s�����ֵ��
��3����ͼ2����AB���е�ΪE����DF��BC������ΪF������CD��CE���Ƿ���ڵ�D��ʹ����C��D��F����Ϊ��������������CEO���ƣ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��30�㣬AB��4��D��F�ֱ���AC��BC���е㣬����ֱ��������DEH�ı�DE������F��EH��BC�ڵ�G����DF��2EF����CG�ij�Ϊ��������
A. 2![]() B. 2
B. 2![]() ��1C.
��1C. ![]() D.
D. ![]() +1
+1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com