
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁїABCЮЊRtЁїЃЌЁЯACBЃН90ЁуЃЌЕуDЮЊABЕФжаЕуЃЌЕуEЮЊБпACЩЯЕФЕуЃЌСЌНсDEЃЌЙ§ЕуEзїEFЁЭEDНЛBCгкFЃЌвдDEЃЌEFЮЊСкБпзїОиаЮDEFGЃЌвбжЊACЃН8ЃЎ
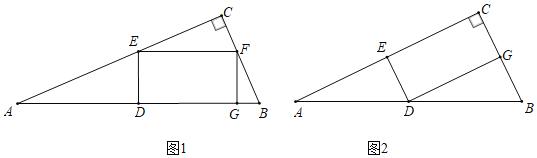
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌЕБBCЃН6ЃЌЕуGдкБпABЩЯЪБЃЌЧѓDEЕФГЄЃЎ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃЌШє![]() ЃЌЕуGдкБпBCЩЯЪБЃЌЧѓBCЕФГЄЃЎ
ЃЌЕуGдкБпBCЩЯЪБЃЌЧѓBCЕФГЄЃЎ
ЃЈ3ЃЉЂйШє![]() ЃЌЧвЕуGЧЁКУТфдкRtЁїABCЕФБпЩЯЃЌЧѓBCЕФГЄЃЎ
ЃЌЧвЕуGЧЁКУТфдкRtЁїABCЕФБпЩЯЃЌЧѓBCЕФГЄЃЎ
ЂкШє![]() ЃЈnЮЊе§ећЪ§ЃЉЃЌЧвЕуGЧЁКУТфдкRtЁїABCЕФБпЩЯЃЌЧыжБНгаДГіBCЕФГЄЃЎ
ЃЈnЮЊе§ећЪ§ЃЉЃЌЧвЕуGЧЁКУТфдкRtЁїABCЕФБпЩЯЃЌЧыжБНгаДГіBCЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉDEЃН![]() ЃЛЃЈ2ЃЉBCЃН4ЃЎЃЈ3ЃЉЂйBCЃН2ЃЌBCЃН8
ЃЛЃЈ2ЃЉBCЃН4ЃЎЃЈ3ЃЉЂйBCЃН2ЃЌBCЃН8![]() -16ЃЌЂкBCЃН
-16ЃЌЂкBCЃН![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЙиЯЕЪНtanЁЯAЃН![]() ЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЩшDEЃНxЃЌдђEFЃНECЃН2xЃЎжЄУїAEЃНECЃЌBCЃН2DEМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЂйЗжЕуGдкBCЛђABЩЯСНжжЧщаЮЗжБ№ЧѓНтЃЎЂкНтЗЈРрЫЦЂйЃЎ
ЃЈ1ЃЉШчЭМ1жаЃЌ

дкRtЁїABCжаЃЌЁпACЃН8ЃЌBCЃН6ЃЌ
ЁрABЃН![]() ЃН10ЃЌ
ЃН10ЃЌ
ЁпDЪЧABжаЕуЃЌ
ЁрADЃНDBЃН5ЃЌ
ЁпЁЯAЃНЁЯAЃЌ
ЁрtanЁЯAЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЩшDEЃНxЃЌдђEFЃНECЃН2xЃЎ
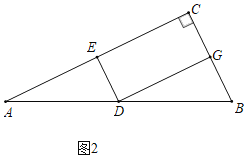
ЁпDEЁЮBCЃЌADЃНDBЃЌ
ЁрAEЃНECЃН2xЃЌ
Ёр4xЃН8ЃЌ
ЁрxЃН2ЃЌ
ЁрDEЃН![]() BCЃЌ
BCЃЌ
ЁрBCЃН2DEЃН4ЃЎ
ЃЈ3ЃЉЂйЕБЕуGТфдкBCБпЩЯЪБЃЌШчЭМ2жаЃЌЩшDEЃНxЃЌдђEFЃНECЃН4xЃЌ
ПЩЕУЃКAEЃНECЃН4xЃЌ8xЃН8ЃЌ
ЁрxЃН1ЃЌ
ЁрBCЃН2DEЃН2ЃЎ
ЕБЕуGТфдкABБпЩЯЪБЃЌ
зїDHЁЭACгкHЃЌЩшDHЃНxЃЌдђCEЃН4xЃЌBCЃН2xЃЌEHЃН4Љ4xЃЌ
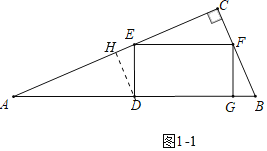
РћгУЁїHDEЁзЁїCABЃЌПЩЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
ЂкШє![]() ЃЈnЮЊе§ећЪ§ЃЉЪБЃЌЭЌЗЈПЩжЊЃК
ЃЈnЮЊе§ећЪ§ЃЉЪБЃЌЭЌЗЈПЩжЊЃК![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕк 24 НьЖЌАТЛсНЋгк 2022 ФъдкББОЉКЭеХМвПкОйааЃЌЖЌАТЛсЕФЯюФПгаЛЌбЉЃЈШчЬјЬЈЛЌбЉЁЂИпЩНЛЌбЉЁЂЕЅАхЛЌбЉЕШЃЉЁЂЛЌБљЃЈШчЖЬЕРЫйЛЌЁЂЫйЖШЛЌБљЁЂЛЈбљЛЌБљЕШЃЉЁЂБљЧђЁЂБљКјЕШЃЎШчЭМЃЌга 5 еХаЮзДЁЂДѓаЁЁЂжЪЕиОљЯрЭЌЕФПЈЦЌЃЌе§УцЗжБ№гЁгаИпЩНЛЌбЉЁЂЫйЖШЛЌБљЁЂБљЧђЁЂЕЅАхЛЌбЉЁЂБљКјЮхжжВЛЭЌЕФЭМАИЃЌБГУцЭъШЋЯрЭЌЃЎЯжНЋет 5 еХПЈЦЌЯДдШКѓе§УцЯђЯТЗХдкзРзгЩЯЃЌДгжаЫцЛњГщШЁвЛеХЃЌГщГіЕФПЈЦЌе§УцЧЁКУЪЧЛЌбЉЯюФПЭМАИЕФИХТЪЪЧЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкЦНУцжБНЧзјБъЯЕжагаСНЕуAЃЈ0ЃЌ1ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌЖЏЕуPдкЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЩЯдЫЖЏЃЌЕБЯпЖЮPAгыЯпЖЮPBжЎВюЕФОјЖджЕзюДѓЪБЃЌЕуPЕФзјБъЮЊ_____ЃЎ
ЕФЭМЯѓЩЯдЫЖЏЃЌЕБЯпЖЮPAгыЯпЖЮPBжЎВюЕФОјЖджЕзюДѓЪБЃЌЕуPЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧАыдВOЕФжБОЖЃЌDЮЊАыдВЩЯЕФЕуЃЌдкBAбгГЄЯпЩЯШЁЕуCЃЌЪЙЕУDCЃНDOЃЌСЌНсCDВЂбгГЄНЛдВOгкЕуEЃЌСЌНсAEЃЌШєЁЯCЃН18ЁуЃЌдђЁЯEABЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ

A. 18ЁуB. 21ЁуC. 27ЁуD. 36Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПJackЭЌбЇКЎМйШЅвАЩњЖЏЮядАгЮЭцЃЌДгBaiduЕиЭМВщевЯпТЗЗЂЯжЃЌМИЬѕЯпТЗОљвЊЛЛГЫЃЌГЫГЕЗНАИШчЯТЃКдкГіЗЂеОЕуПЩбЁдёПеЕїГЕAЃЌПеЕїГЕBЃЌЦеЭЈГЕaЃЛЛЛГЫЕуПЩбЁдёПеЕїГЕCЃЌЦеЭЈГЕbЃЌЦеЭЈГЕcЃЌЫљгаГЕСООљдкЭЌвЛеОЕуЛЛГЫЃЎ
ЃЈ1ЃЉЧѓJackЭЌбЇдкГіЗЂЕуГЫзјПеЕїГЕЕФИХТЪЃЛ
ЃЈ2ЃЉвбжЊПеЕїГЕЦБМл2дЊЃЌЦеЭЈГЕЦБМл1дЊЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓJackЭЌбЇЕНДяЖЏЮядАЧЁКУЛЈЗб3дЊЙЋНЛЗбЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
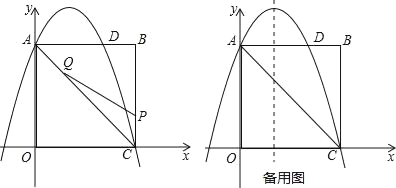
ЁОЬтФПЁПШчЭМЃЌдкОиаЮOABCжаЃЌЕуOЮЊдЕуЃЌЕуAЕФзјБъЮЊ(0ЃЌ8)ЃЌЕуCЕФзјБъЮЊ(6ЃЌ0)ЃЎХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§ЕуAЁЂCЃЌгыABНЛгкЕуDЃЎ
x2+bx+cОЙ§ЕуAЁЂCЃЌгыABНЛгкЕуDЃЎ
(1)ЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
(2)ЕуPЮЊЯпЖЮBCЩЯвЛИіЖЏЕу(ВЛгыЕуCжиКЯ)ЃЌЕуQЮЊЯпЖЮACЩЯвЛИіЖЏЕуЃЌAQЃНCPЃЌСЌНгPQЃЌЩшCPЃНmЃЌЁїCPQЕФУцЛ§ЮЊSЃЎ
ЂйЧѓSЙигкmЕФКЏЪ§БэДяЪНЃЛ
ЂкЕБSзюДѓЪБЃЌдкХзЮяЯпyЃНЉ![]() x2+bx+cЕФЖдГЦжсlЩЯЃЌШєДцдкЕуFЃЌЪЙЁїDFQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
x2+bx+cЕФЖдГЦжсlЩЯЃЌШєДцдкЕуFЃЌЪЙЁїDFQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
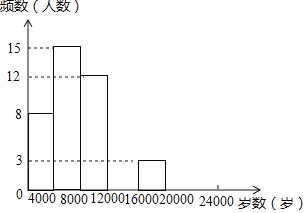
ЁОЬтФПЁПЯжНёЁАЮЂаХдЫЖЏЁББЛдНРДдНЖрЕФШЫЙизЂКЭЯВАЎЃЌФГаЫШЄаЁзщЫцЛњЕїВщСЫЮвЪа50УћНЬЪІФГШеЁАЮЂаХдЫЖЏЁБжаЕФВНЪ§ЧщПіНјааЭГМЦећРэЃЌЛцжЦСЫШчЯТЕФЭГМЦЭМБэЃЈВЛЭъећЃЉЃК
ВНЪ§ | ЦЕЪ§ | ЦЕТЪ |
0ЁмxЃМ4000 | 8 | a |
4000ЁмxЃМ8000 | 15 | 0.3 |
8000ЁмxЃМ12000 | 12 | b |
12000ЁмxЃМ16000 | c | 0.2 |
16000ЁмxЃМ20000 | 3 | 0.06 |
20000ЁмxЃМ24000 | d | 0.04 |
ЧыИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіaЃЌbЃЌcЃЌdЕФжЕВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉБОЪадМга37800УћНЬЪІЃЌгУЕїВщЕФбљБОЪ§ОнЙРМЦШеаазпВНЪ§ГЌЙ§12000ВНЃЈАќКЌ12000ВНЃЉЕФНЬЪІгаЖрЩйУћЃП
ЃЈ3ЃЉШєдк50УћБЛЕїВщЕФНЬЪІжаЃЌбЁШЁШеаазпВНЪ§ГЌЙ§16000ВНЃЈАќКЌ16000ВНЕФСНУћНЬЪІгыДѓМвЗжЯэаФЕУЃЌЧѓБЛбЁШЁЕФСНУћНЬЪІЧЁКУЖМдк20000ВНЃЈАќКЌ20000ВНЃЉвдЩЯЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЮЊСЫИФЩЦАьбЇЬѕМўЃЌМЦЛЎЙКжУвЛХњЕчзгАзАхКЭЬЈЪНЕчФдЃЎОеаЭЖБъЃЌЙКТђвЛЬЈЕчзгАзАхБШЙКТђ2ЬЈЬЈЪНЕчФдЖр3000дЊЃЌЙКТђ2ЬЈЕчзгАзАхКЭ3ЬЈЬЈЪНЕчФдЙВаш2.7ЭђдЊЃЎ
ЃЈ1ЃЉЧѓЙКТђвЛЬЈЕчзгАзАхКЭвЛЬЈЬЈЪНЕчФдИїашЖрЩйдЊЃП
ЃЈ2ЃЉИљОнИУаЃЪЕМЪЧщПіЃЌЙКТђЕчзгАзАхКЭЬЈЪНЕчФдЕФзмЬЈЪ§ЮЊ24ЃЌВЂЧвЬЈЪНЕчФдЕФЬЈЪ§ВЛГЌЙ§ЕчзгАзАхЬЈЪ§ЕФ3БЖЃЎЮЪдѕбљЙКТђзюЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
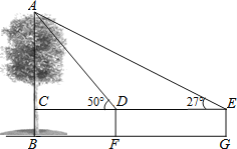
ЁОЬтФПЁПФГЪ§бЇаЫШЄаЁзщгУИпЮЊ1.2УзЕФВтНЧвЧВтСПаЁЪїABЕФИпЖШЃЌШчЭМЃЌдкОрABвЛЖЈОрРыЕФFДІВтЕУаЁЪїЖЅВПAЕФбіНЧЮЊ50ЁуЃЌбиBFЗНЯђаазп3.5УзЕНGДІЪБЃЌгжВтЕУаЁЪїЖЅВПAЕФбіНЧЮЊ27ЁуЃЌЧѓаЁЪїABЕФИпЖШЃЎЃЈВЮПМЪ§ОнЃКsin27Ёу=0.45ЃЌcos27Ёу=0.89ЃЌtan27Ёу=0.5ЃЌsin50Ёу=0.77ЃЌcos50Ёу=0.64ЃЌtan50Ёу=1.2ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com