
【题目】Jack同学寒假去野生动物园游玩,从Baidu地图查找线路发现,几条线路均要换乘,乘车方案如下:在出发站点可选择空调车A,空调车B,普通车a;换乘点可选择空调车C,普通车b,普通车c,所有车辆均在同一站点换乘.
(1)求Jack同学在出发点乘坐空调车的概率;
(2)已知空调车票价2元,普通车票价1元,请用树状图或列表法求Jack同学到达动物园恰好花费3元公交费的概率.
科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为400人,如表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类 | 频数 | 频率 |
科普常识 | 1600本 | B |
名人传记 | 1280本 | 0.32 |
漫画丛书 | A本 | 0.24 |
其它 | 160本 | 0.04 |
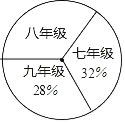
(1)求该校八年级的人数占全校总人数的百分率为 ;
(2)表中A= ,B= ;
(3)该校学生平均每人读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+2
x2+2![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,对称轴与x轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交x轴交于点G.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,对称轴与x轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交x轴交于点G.
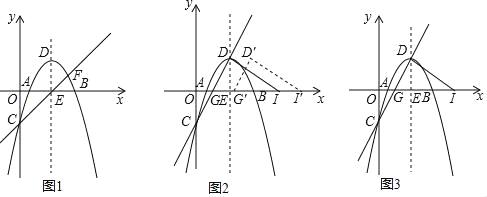
(1)如图1,求直线CE的解析式和顶点D的坐标;
(2)如图1,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于x轴的直线l上一点,点N是抛物线对称轴上一点,求FM+MN+NO的最小值;
(3)如图2,过点D作DI⊥DG交x轴于点I,将△GDI沿射线GB方向平移至△G′D′I′处,将△G′D′I′绕点D′逆时针旋转α(0<α<180°),当旋转到一定度数时,点G′会与点I重合,记旋转过程中的△G′D′I′为△G″D′I″,若在整个旋转过程中,直线G″I″分别交x轴和直线GD′于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:

①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC为Rt△,∠ACB=90°,点D为AB的中点,点E为边AC上的点,连结DE,过点E作EF⊥ED交BC于F,以DE,EF为邻边作矩形DEFG,已知AC=8.
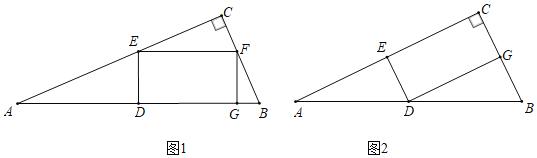
(1)如图1所示,当BC=6,点G在边AB上时,求DE的长.
(2)如图2所示,若![]() ,点G在边BC上时,求BC的长.
,点G在边BC上时,求BC的长.
(3)①若![]() ,且点G恰好落在Rt△ABC的边上,求BC的长.
,且点G恰好落在Rt△ABC的边上,求BC的长.
②若![]() (n为正整数),且点G恰好落在Rt△ABC的边上,请直接写出BC的长.
(n为正整数),且点G恰好落在Rt△ABC的边上,请直接写出BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
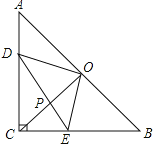
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为![]() ;④
;④![]() ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com