
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且点
两点,且点![]() ,点
,点![]() 在
在![]() 轴正半轴上运动,过点
轴正半轴上运动,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
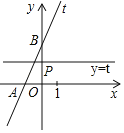
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)当![]() 时,直线
时,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)当![]() 时,若直线
时,若直线![]() 与直线
与直线![]() 和(2)反比例函数的图象分别交于点
和(2)反比例函数的图象分别交于点![]() ,
,![]() ,当
,当![]() 间距离大于等于2时,求
间距离大于等于2时,求![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx﹣3与双曲线![]() 的两个交点为A,B,其中A(﹣1,m).
的两个交点为A,B,其中A(﹣1,m).
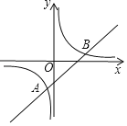
(1)求m的值及直线的表达式;
(2)若点M为x轴上一个动点,且△AMB为直角三角形,直接写出满足条件的点M的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )
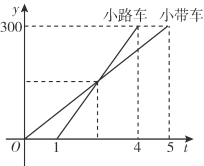
A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径CD=4,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=2![]() ,则∠ACD等于( )
,则∠ACD等于( )
A.30°B.60°C.30°或60°D.45°或60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG.
求证:ED=EC.
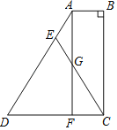
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求该抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 平行于
平行于![]() 轴,交
轴,交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,试求出线段
,试求出线段![]() 的最大值,并写出此时点
的最大值,并写出此时点![]() 的坐标;
的坐标;
(3)抛物线上是否存在一点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com