
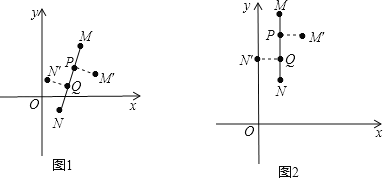
【题目】在平面直角坐标系xOy中,对于线段MN的“三等分变换”,给出如下定义:如图1,点P,Q为线段MN的三等分点,即MP=PQ=QN,将线段PM以点P为旋转中心顺时针旋转90°得到PM′,将线段QN以点Q为旋转中心顺时针旋转90°得到QN′,则称线段MN进行了三等分变换,其中M′,N′记为点M,N三等分变换后的对应点.
例如:如图2,线段MN,点M的坐标为(1,5),点N的坐标为(1,2),则点P的坐标为(1,4),点Q的坐标为(1,3),那么线段MN三等分变换后,可得:M′的坐标为(2,4),点N′的坐标为(0,3).
(1)若点P的坐标为(2,0),点Q的坐标为(4,0),直接写出点M′与点N′的坐标;
(2)若点Q的坐标是(0,﹣![]() ),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
(3)若点Q的坐标为(0,0),点M′的坐标为(﹣3,﹣3),直接写出点P与点N的坐标;
(4)点P是以原点O为圆心,1为半径的圆上的一个定点,点P的坐标为(![]() ,
,![]() )当点N′在圆O内部或圆上时,求线段PQ的取值范围及PQ取最大值时点M′的坐标.
)当点N′在圆O内部或圆上时,求线段PQ的取值范围及PQ取最大值时点M′的坐标.
【答案】(1)M(2,2),N′(4,﹣2);(2)![]() ;(3)P(0,﹣3),N(0,3);(4)(
;(3)P(0,﹣3),N(0,3);(4)(![]() ,
,![]() )
)
【解析】
(1)根据“三等分变换”的定义,可知M(2,2),N′(4,﹣2);(2)若点Q的坐标是(0,﹣![]() ),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
),点P在x轴正半轴上,点N′在第二象限.当线段PQ的长度为符合条件的最小整数时,求OP的长;
(3)若点Q的坐标为(0,0),点M′的坐标为(﹣3,﹣3),直接写出点P与点N的坐标;(4)如图3中,过点P作PA⊥x轴于点A.在Rt△OAP中,由勾股定理,OP=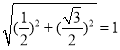 ,在△PQN′中,∠PQN′=90°,PQ=QN′,推出点N′在⊙O内部或在⊙O上运动,当PN′为⊙O直径时,PN′最大,推出∠QPN′=45°推出PQ=PN′=
,在△PQN′中,∠PQN′=90°,PQ=QN′,推出点N′在⊙O内部或在⊙O上运动,当PN′为⊙O直径时,PN′最大,推出∠QPN′=45°推出PQ=PN′=![]() ,推出PQ的取值范围:0<PQ≤
,推出PQ的取值范围:0<PQ≤![]() ,由P(
,由P(![]() ,﹣
,﹣![]() ),由对称性可知N′(﹣
),由对称性可知N′(﹣![]() ,
,![]() ),再根据平行四边形的性质求出点M′坐标即可.
),再根据平行四边形的性质求出点M′坐标即可.
解:(1)∵PQ=2,根据“三等分变换”的定义,可知M(2,2),N′(4,﹣2).
(2)①当PQ=1时,OQ=![]()
在RT△OPQ中,如图1中,
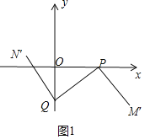
∴OP=OQ
∴∠OQP=∠OPQ=45°
∵∠PQN′=90°PQ=Q N′
∴点N’在x轴负半轴上,不在第二象限
∴PQ=1不符合题意.
②当PQ=2时
OP=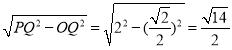 ,
,
此时,点N′在第二象限符合题意.
(3)如图2中,由图象可知,P(0,﹣3),N(0,3).
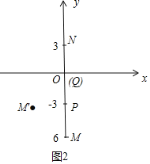
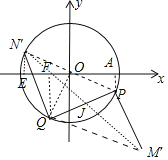
(4)如图3中,过点P作PA⊥x轴于点A.
在Rt△OAP中,由勾股定理,OP=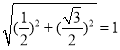 ,
,
在△PQN′中,∠PQN′=90°,PQ=QN'
点N'在⊙O内部或在⊙O上运动,当PN′为⊙O直径时,PN′最大
∠QPN′=45°
∴PQ=PN′=![]() ,
,
∴PQ的取值范围:0<PQ≤![]() ,
,
∵P(![]() ,﹣
,﹣![]() )
)
由对称性可知N′(﹣![]() ,
,![]() )
)
过点N′作N′E⊥x轴于点E,过点Q作QF⊥x轴于点F
易证△ON′E≌△QOF,
∴OF=EN′=![]() ,FQ=OE=
,FQ=OE=![]()
∴Q(﹣![]() ,﹣
,﹣![]() )
)
∵∠N′QP=∠QP M′=90°
∴N′Q∥PM′,
又∵N′Q=PM′,
∴四边形PN′QM′是平行四边形,对角线的交点为J,设M′(m,n)
则J(![]() ,﹣
,﹣![]() ),
),
则有 ,
, ,
,
解得![]() ,
,![]() ,
,
∴点M′的坐标为(![]() ,
,![]() ).
).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子频率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:①种子个数是700时,发芽种子的个数是624.所以种子发芽的概率是0.891;②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性.可以估计种子发芽的概率约为0.9(精确到0.1);③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子大约有
种子大约有![]() 的种子不能发芽.其中合理的是( )
的种子不能发芽.其中合理的是( )
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
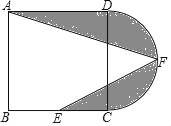
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
科目:初中数学 来源: 题型:
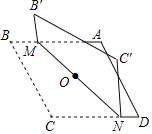
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B的对应点为B',C的对应点为C',MN是折痕若B'M=1,则CN的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校需要购买A、B两种品牌的篮球,购买A种品牌的篮球30个,B种品牌的篮球20个,共花费5400元,已知购买一个B种品牌的篮球比购买一个A钟品牌的篮球多花20元.
(1)求购买一个A种品牌、一个B种品牌的篮球各需多少元?
(2)学校为了响应习“篮球进校园”的号召,决定再次购进A、B两种品牌球共45个,正好是上商场对商品的促销活动,A品牌篮球售价比第一次购买时降低19元,B品牌篮球按第一次购买时售价的9折出售,如果学校此次购买A、B两种品牌篮球的总费用不超过第一次花费的80%,且保证这次购买的B种品牌篮球不少于15个,则这次学校有几种购买方案?
(3)学校在第二次购买活动中至少需要多少资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象与直线y=2x+1交于点A(1,m).
的图象与直线y=2x+1交于点A(1,m).
(1)求k、m的值;
(2)已知点P(n,0)(n≥1),过点P作平行于y轴的直线,交直线y=2x+1于点B,交函数![]() 的图象于点C.横、纵坐标都是整数的点叫做整点.
的图象于点C.横、纵坐标都是整数的点叫做整点.
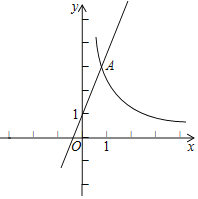
①当n=3时,求线段AB上的整点个数;
②若![]() 的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
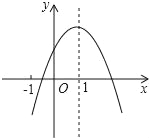
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com