
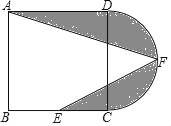
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
【答案】C
【解析】作FH⊥BC于H,连接FH,如图,根据正方形的性质和切线的性质得BE=CE=CH=FH=6,则利用勾股定理可计算出AE=6![]() ,通过Rt△ABE≌△EHF得∠AEF=90°,然后利用图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF进行计算.
,通过Rt△ABE≌△EHF得∠AEF=90°,然后利用图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF进行计算.
作FH⊥BC于H,连接FH,如图,
∵点E为BC的中点,点F为半圆的中点,
∴BE=CE=CH=FH=6,
AE=![]() =6
=6![]() ,
,
易得Rt△ABE≌△EHF,
∴∠AEB=∠EFH,
而∠EFH+∠FEH=90°,
∴∠AEB+∠FEH=90°,
∴∠AEF=90°,
∴图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF
=12×12+![]() π62﹣
π62﹣![]() ×12×6﹣
×12×6﹣![]() 6
6![]() ×6
×6![]()
=18+18π.
故选:C.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:初中数学 来源: 题型:
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
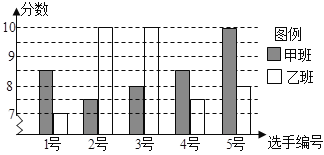
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
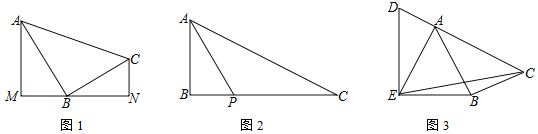
【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,CD是△ACB的角平分线.若在边AC上截取CE=CB,连接DE,则图中等腰三角形共有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
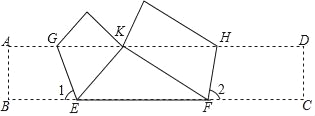
【题目】如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=![]() +1,求BC的长.
+1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件是( )

A. AD=BC
B. AC=BD
C. AB=CD
D. AD=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
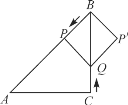
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,点P从点B出发,沿BA方向以每秒![]() cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一次函数y=(1-3k)x+2k-1,试回答:
(1)k为何值时,y随x的增大而减小?
(2)k为何值时,图像与y轴交点在x轴上方?
(3) 若一次函数y=(1-3k)x+2k-1经过点(3,4).请求出一次函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com