
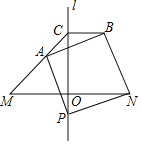
【题目】如图,直线l是线段MN的垂直平分线,交线段MN于点O,在MN下方的直线l上取一点P,连接PN,以线段PN为边,在PN上方作正方形NPAB,射线MA交直线l于点C,连接BC.
(1)设∠ONP=α,求∠AMN的度数;
(2)写出线段AM、BC之间的等量关系,并证明.
【答案】(1)45°(2)![]() ,理由见解析
,理由见解析
【解析】
(1)由线段的垂直平分线的性质可得PM=PN,PO⊥MN,由等腰三角形的性质可得∠PMN=∠PNM=α,由正方形的性质可得AP=PN,∠APN=90°,可得∠APO=α,由三角形内角和定理可求∠AMN的度数;
(2)由等腰直角三角形的性质和正方形的性质可得![]() ,
,![]() ,∠MNC=∠ANB=45°,可证△CBN∽△MAN,可得
,∠MNC=∠ANB=45°,可证△CBN∽△MAN,可得![]() .
.
解:(1)如图,连接MP,
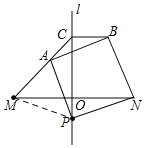
∵直线l是线段MN的垂直平分线,
∴PM=PN,PO⊥MN
∴∠PMN=∠PNM=α
∴∠MPO=∠NPO=90°-α,
∵四边形ABNP是正方形
∴AP=PN,∠APN=90°
∴AP=MP,∠APO=90°-(90°-α)=α
∴∠APM=∠MPO-∠APO=(90°-α)-α=90°-2α,
∵AP=PM
∴![]() ,
,
∴∠AMN=∠AMP-∠PMN=45°+α-α=45°
(2)![]()
理由如下:
如图,连接AN,CN,

∵直线l是线段MN的垂直平分线,
∴CM=CN,
∴∠CMN=∠CNM=45°,
∴∠MCN=90°
∴![]() ,
,
∵四边形APNB是正方形
∴∠ANB=∠BAN=45°
∴![]() ,∠MNC=∠ANB=45°
,∠MNC=∠ANB=45°
∴∠ANM=∠BNC
又∵![]()
∴△CBN∽△MAN
∴![]()
∴![]()


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
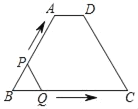
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,点P从点B出发沿折线BA﹣AD﹣DC匀速运动,同时,点Q从点B出发沿折线BC﹣CD匀速运动,点P与点Q的速度相同,当二者相遇时,运动停止,设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A. B.
B.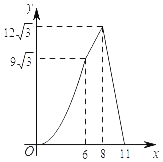
C.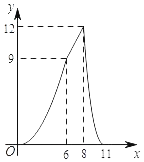 D.
D.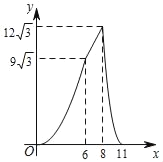
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子频率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:①种子个数是700时,发芽种子的个数是624.所以种子发芽的概率是0.891;②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性.可以估计种子发芽的概率约为0.9(精确到0.1);③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子大约有
种子大约有![]() 的种子不能发芽.其中合理的是( )
的种子不能发芽.其中合理的是( )
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,且
,且![]() ,
,![]() ,我们规定:如果存在点P,使
,我们规定:如果存在点P,使![]() 是以线段MN为直角边的等腰直角三角形,那么称点P为点M、N的“和谐点”.
是以线段MN为直角边的等腰直角三角形,那么称点P为点M、N的“和谐点”.
(1)已知点A的坐标为![]() ,
,
①若点B的坐标为![]() ,在直线AB的上方,存在点A,B的“和谐点”C,直接写出点C的坐标;
,在直线AB的上方,存在点A,B的“和谐点”C,直接写出点C的坐标;
②点C在直线x=5上,且点C为点A,B的“和谐点”,求直线AC的表达式.
(2)⊙O的半径为r,点![]() 为点
为点![]() 、
、![]() 的“和谐点”,且DE=2,若使得
的“和谐点”,且DE=2,若使得![]() 与⊙O有交点,画出示意图直接写出半径r的取值范围.
与⊙O有交点,画出示意图直接写出半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
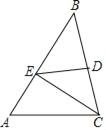
【题目】已知如图,在△ABC中,∠B=45°,点D是BC边的中点,DE⊥BC于点D,交AB于点E,连接CE.
(1)求∠AEC的度数;
(2)请你判断AE、BE、AC三条线段之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲打字员计划用若干小时完成文稿的电脑输入工作,两小时后,乙打字员协助此项工作,且乙打字员文稿电脑输入的速度是甲的1.5倍,结果提前6小时完成任务,则甲打字员原计划完成此项工作的时间是( )
A.17小时B.14小时C.12小时D.10小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
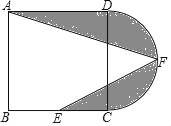
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
科目:初中数学 来源: 题型:
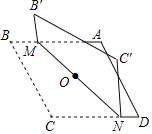
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B的对应点为B',C的对应点为C',MN是折痕若B'M=1,则CN的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
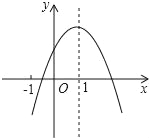
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com