
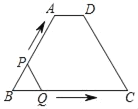
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,点P从点B出发沿折线BA﹣AD﹣DC匀速运动,同时,点Q从点B出发沿折线BC﹣CD匀速运动,点P与点Q的速度相同,当二者相遇时,运动停止,设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A.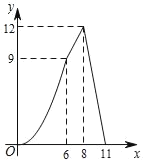 B.
B.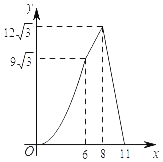
C.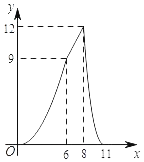 D.
D.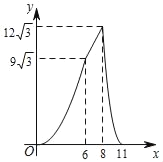
【答案】B
【解析】
①当点P在AB上运动时(0≤x≤6),![]() ,当x=6时,
,当x=6时,![]() ; ②6<x<8,
; ②6<x<8,![]() ;③当x≥8时,点PC=6+2+6-x=14-x,QC= 8-x,则PQ=22-2t,△BPQ的高常数,即可求解.
;③当x≥8时,点PC=6+2+6-x=14-x,QC= 8-x,则PQ=22-2t,△BPQ的高常数,即可求解.
解:由题意得:四边形ABCD为等腰梯形,如下图,分别过点A、D作梯形的高AM、DN交BC于点M、N,
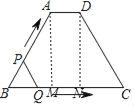
则MN=AD=2,BM=NC=![]() (BC﹣AD)=3,
(BC﹣AD)=3,
则AB=2BM=6,
①当点P在AB上运动时(0≤x≤6),
![]() ,
,
当x=6时,y=9![]() ,
,
图象中符合条件的有B、D;
②6<x<8,高为常数,
∵MN=AD=2,BM=![]() (BC- MN)=3,
(BC- MN)=3,
∴AM=BMtanB=3×![]() =3
=3![]() ,
,
则![]() ;
;
③当x≥8时,点PC=6+2+6﹣x=14﹣x,QC=x﹣8,
则PQ=22﹣2x,
而△BPQ的高常数,故y的表达式为一次函数,
故在B、D中符合条件的为B,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:

(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60°时,PM的长度约为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是 ;
(2)如表是y与x的几组对应数值:
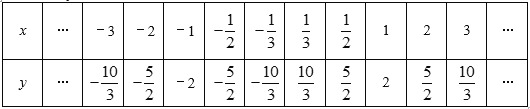
在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
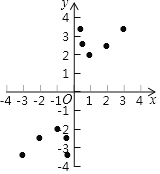
(3)进一步探究发现:该函数在第一象限内的最低点的坐标是(1,2),观察函数图象,写出该函数的另一条性质 ;
(4)请你利用配方法证明:当x>0时,![]() 最小值为2.(提示:当x>0时
最小值为2.(提示:当x>0时![]() ,
,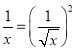 ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
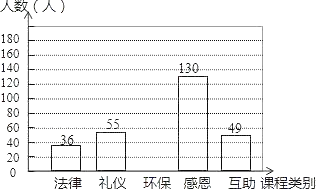
【题目】某校有学生3600人,在“文明我先行”的活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了一些学生,并制成统计表和统计图:
课程类别 | 频数 | 频率 |
法律 | 36 | 0.09 |
礼仪 | 55 | 0.1375 |
环保 | m | a |
感恩 | 130 | 0.325 |
互助 | 49 | 0.1225 |
合计 | n | 1.00 |
(1)在这次调查活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”)a= ,m= ,n= .
(2)请补全条形统计图,如果要画一个“校本课程报名意向扇形统计图”,那么“环保”类校本课程所对应的扇形圆心角应为 度;
(3)请估算该校3600名学生中选择“感恩”校本课程的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游团于早上8:00从某旅行社出发,乘大巴车前往“珠海长隆”旅游,“珠海长隆”离该旅行社有100千米,导游张某因有事情,于8:30从该旅行社自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比该旅游团提前20分钟到达“珠海长隆”.
(1)大巴与小车的平均速度各是多少?
(2)导游张某追上大巴的地点到“珠海长隆”的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
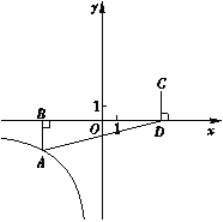
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的.讲课开始时,学生的注意力激增,中间有一段时间,学生的注意力保持平稳状态,随后开始分散.学生注意力指标数![]() 随时间
随时间![]() 变化的函数图象如图所示(
变化的函数图象如图所示(![]() 越大表示学生注意力越集中).当
越大表示学生注意力越集中).当![]() 时,图象是抛物线的一部分;当
时,图象是抛物线的一部分;当![]() 和
和![]() 时,图象是线段.根据图象回答问题:
时,图象是线段.根据图象回答问题:
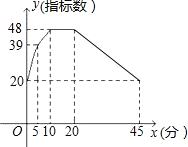
(1)课堂上,学生注意力保持平稳状态的时间段是_______.
(2)结合函数图象回答,一道几何综合题如果需要讲25分钟,老师最好在上课后大约第______分钟到第________分钟讲这道题,能使学生处于注意力比较集中的听课状态.
查看答案和解析>>
科目:初中数学 来源: 题型:
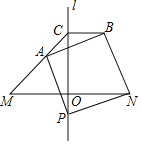
【题目】如图,直线l是线段MN的垂直平分线,交线段MN于点O,在MN下方的直线l上取一点P,连接PN,以线段PN为边,在PN上方作正方形NPAB,射线MA交直线l于点C,连接BC.
(1)设∠ONP=α,求∠AMN的度数;
(2)写出线段AM、BC之间的等量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com