
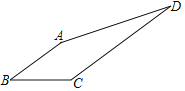
【题目】如图,在四边形ABCD中,AB∥CD,2AB=2BC=CD=10,tanB=![]() ,则AD=______.
,则AD=______.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】问题:将菱形的面积五等分.小红发现只要将菱形周长五等分,再将各分点与菱形的对角线交点连接即可解决问题.如图,点O是菱形ABCD的对角线交点,AB=5,下面是小红将菱形ABCD面积五等分的操作与证明思路,请补充完整.
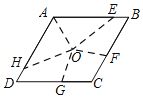
(1)在AB边上取点E,使AE=4,连接OA,OE;
(2)在BC边上取点F,使BF=______,连接OF;
(3)在CD边上取点G,使CG=______,连接OG;
(4)在DA边上取点H,使DH=______,连接OH.由于AE=______+______=______+______=______+______=______.可证S△AOE=S四边形EOFB=S四边形FOGC=S四边形GOHD=S△HOA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是![]() ,
,![]() .
.
![]() 对于坐标平面内的一点P,给出如下定义:如果
对于坐标平面内的一点P,给出如下定义:如果![]() ,则称点P为线段AB的“等角点”
,则称点P为线段AB的“等角点”![]() 显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
![]() 设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和
设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和![]() 的半径;
的半径;
![]() 轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
![]() 当点P在y轴正半轴上运动时,
当点P在y轴正半轴上运动时,![]() 是否有最大值?如果有,说明此时
是否有最大值?如果有,说明此时![]() 最大的理由,并求出点P的坐标;如果没有请说明理由.
最大的理由,并求出点P的坐标;如果没有请说明理由.
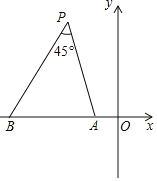
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0),(1)求抛物线的解析式_____.(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P′,当点P′落在第二象限内,P′A2取得最小值时,求m的值_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
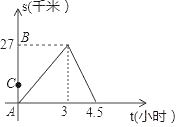
【题目】某电视台摄制组乘船往返于A码头和B码头进行拍摄,在A、B两码头间设置拍摄中心C.在往返过程中,假设船在A、B、C处均不停留,船离开B码头的距离s(千米)与航行的时间t(小时)之间的函数关系式如图所示.根据图象信息,解答下列问题:
(1)求船从B码头返回A码头时的速度及返回时s关于t的函数表达式.
(2)求水流的速度.
(3)若拍摄中心C设在离A码头12千米处,摄制组在拍摄中心分两组拍摄,其中一组乘橡皮艇漂流到B码头处,另一组同时乘船到达A码头后马上返回,求两摄制组相遇时离拍摄中心C的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
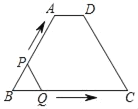
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,点P从点B出发沿折线BA﹣AD﹣DC匀速运动,同时,点Q从点B出发沿折线BC﹣CD匀速运动,点P与点Q的速度相同,当二者相遇时,运动停止,设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A.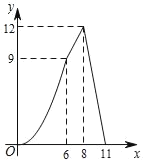 B.
B.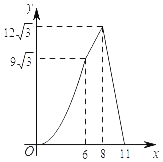
C.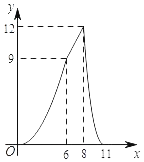 D.
D.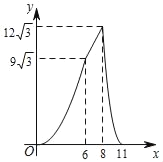
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:
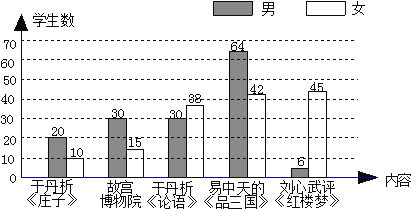
请根据统计图提供的信息回答以下问题:
(1)这一调查属于_______(选填“抽样调查”或“普查”),抽取的学生数为_____名;
(2)估计喜欢收听易中天《品三国》的学生约占全校学生的____%(精确到小数点后一位);
(3)已知该校女学生共有1800名,则该校喜欢收听刘心武评《红楼梦》的女学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
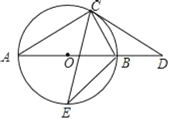
【题目】AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB的延长线相交于点D,CA=CD.
(1)连接BC,求证:BC=OB;
(2)E是![]() 中点,连接CE,BE,若BE=2,求CE的长.
中点,连接CE,BE,若BE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
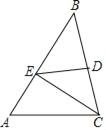
【题目】已知如图,在△ABC中,∠B=45°,点D是BC边的中点,DE⊥BC于点D,交AB于点E,连接CE.
(1)求∠AEC的度数;
(2)请你判断AE、BE、AC三条线段之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com