
【题目】问题:将菱形的面积五等分.小红发现只要将菱形周长五等分,再将各分点与菱形的对角线交点连接即可解决问题.如图,点O是菱形ABCD的对角线交点,AB=5,下面是小红将菱形ABCD面积五等分的操作与证明思路,请补充完整.
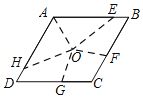
(1)在AB边上取点E,使AE=4,连接OA,OE;
(2)在BC边上取点F,使BF=______,连接OF;
(3)在CD边上取点G,使CG=______,连接OG;
(4)在DA边上取点H,使DH=______,连接OH.由于AE=______+______=______+______=______+______=______.可证S△AOE=S四边形EOFB=S四边形FOGC=S四边形GOHD=S△HOA.
【答案】(1)见解析;(2)3;(3)2;(4)1,EB、BF;FC、CG;GD、DH;HA
【解析】
利用菱形四条边相等,分别在四边上进行截取和连接,得出AE=EB+BF=FC+CG+GD+DH
=HA,进一步求得S△AOE=S四边形EOFB=S四边形FOGC=S四边形GOHD=S△HOA.即可.
(1)在AB边上取点E,使AE=4,连接OA,OE;
(2)在BC边上取点F,使BF=3,连接OF;
(3)在CD边上取点G,使CG=2,连接OG;
(4)在DA边上取点H,使DH=1,连接OH.
由于AE=EB+BF=FC+CG=GD+DH=HA.
可证S△AOE=S四边形EOFB=S四边形FOGC=S四边形GOHD=S△HOA.
故答案为:3,2,1;EB、BF;FC、CG;GD、DH;HA.


科目:初中数学 来源: 题型:
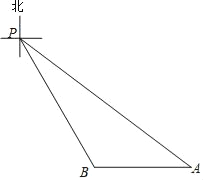
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
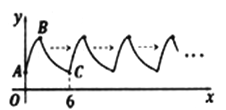
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线 ![]() 的一部分,曲线BC是双曲线
的一部分,曲线BC是双曲线![]() 的一部分,由点C开始不断重复“A-B-C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上,
的一部分,由点C开始不断重复“A-B-C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上, ![]() =_______.
=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图线段OA和折线BCD分别表示两车离甲地的距离y(单位:千米)与时间x(单位:小时)之间的函数关系.则下列说法正确的是( )
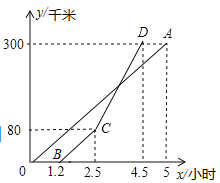
A.两车同时到达乙地
B.轿车在行驶过程中进行了提速
C.货车出发3小时后,轿车追上货车
D.两车在前80千米的速度相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:

(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60°时,PM的长度约为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2.
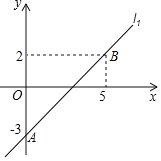
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:如图2,
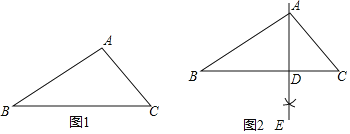
(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.所以线段AD就是所求作的高.
请回答:该尺规作图的依据是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com