
分析 原式通分并利用同分母分式的加减法则计算即可得到结果.
解答 解:原式=$\frac{{x}^{2}+x+1-2{x}^{2}-2x+2}{({x}^{2}+x)^{2}-1}$+$\frac{1}{{x}^{2}+x+3}$=$\frac{(-{x}^{2}-x+3)({x}^{2}+x+3)+{x}^{4}+2{x}^{3}+{x}^{2}-1}{({x}^{4}+2{x}^{3}+{x}^{2}-1)({x}^{2}+x+3)}$=$\frac{8}{({x}^{4}+2{x}^{3}+{x}^{2}-1)({x}^{2}+x+3)}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
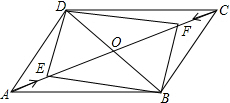 如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?
如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 水果箱的类别 | A | B | C | D | E |
| 与标准质量的差值(单位:千克) | -2 | -1.5 | 0 | 1 | 2.5 |
| 箱数 | 1 | 3 | 1 | 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
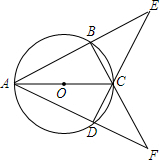 如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.
如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com