
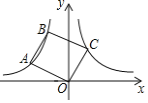
【题目】如图,点A、B在双曲线![]() (x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线
(x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线![]() (x>0)上,此时OABC的面积为( ).
(x>0)上,此时OABC的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.4
D.4![]()
【答案】B
【解析】
连接AC,过A作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,利用AAS证出△ABF≌△COE,设A(a,﹣![]() ),C(b,
),C(b,![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF=![]() ,即可表示出点B的坐标,然后代入反比例函数的解析式中即可求出
,即可表示出点B的坐标,然后代入反比例函数的解析式中即可求出![]() ,然后根据平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可求出结论.
,然后根据平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可求出结论.
解:如图,连接AC,过A作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,

∵FD⊥x轴,CE⊥x轴
∴FD∥CE
∴∠FAC=∠ECA
∵四边形AOCB是平行四边形
∴BA∥OC,BA=OC,∠BAC=∠OCA
∴∠FAB=∠FAC-∠BAC=∠ECA-∠OCA=∠ECO
在△ABF和△COE中
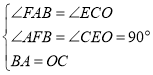
∴△ABF≌△COE,
设A(a,﹣![]() ),C(b,
),C(b,![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF=![]() ,
,
∴B(a+b,﹣![]() ),
),
又∵点B在双曲线y=-![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣![]() )=﹣3,
)=﹣3,
∴![]() ﹣
﹣![]() =2,
=2,
设![]() =x,则方程
=x,则方程![]() ﹣
﹣![]() =2可化为3x﹣
=2可化为3x﹣![]() =2,
=2,
解得x=![]() 或x=
或x=![]() (a和b异号,故舍去),
(a和b异号,故舍去),
∴![]() =
=![]() ,
,
∴![]() =﹣
=﹣![]() ,
,
∴平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[![]() (﹣
(﹣![]() )(b﹣a)﹣
)(b﹣a)﹣![]() ×|﹣3|﹣
×|﹣3|﹣![]() ×|2|]
×|2|]
=﹣![]() +3+2﹣
+3+2﹣![]() ﹣5
﹣5
=﹣3×![]() ﹣2×(﹣
﹣2×(﹣![]() )
)
=2![]() .
.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的![]() 倍,但进价比第一批每件多了5元.
倍,但进价比第一批每件多了5元.
(1)第一批仙桃每件进价是多少元?
(2)老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在一节数学探究课上,学生们发现了一个规律:
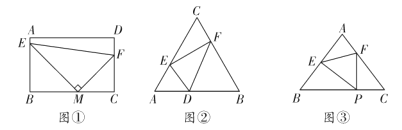
如图①,当四边形![]() 是矩形时,
是矩形时,![]() 的直角顶点M在
的直角顶点M在![]() 边上运动,直角边分别与线段
边上运动,直角边分别与线段![]() 、线段
、线段![]() 交于E、F两点,在点M运动的过程中,始终存在着
交于E、F两点,在点M运动的过程中,始终存在着![]() .于是又有同学提出了问题,如果将四边形换成三角形时,是否仍存在同样的规律呢?如图②,在
.于是又有同学提出了问题,如果将四边形换成三角形时,是否仍存在同样的规律呢?如图②,在![]() 中,
中,![]() ,点D为
,点D为![]() 边上的动点,过点D作
边上的动点,过点D作![]() ,交
,交![]() 于点E,交
于点E,交![]() 于点F,请问是否存在两个相似的三角形,若存在,请证明;若不存在,请说明理由;
于点F,请问是否存在两个相似的三角形,若存在,请证明;若不存在,请说明理由;
(2)结合上述规律,解决下列问题:
如图③,在![]() 中,
中,![]() ,
,![]() ,点P为
,点P为![]() 上一点(不与B、C重合),过点P作
上一点(不与B、C重合),过点P作![]() 于点E,
于点E,![]() 交
交![]() 于点F,若
于点F,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个由1~28的连续整数排成的“数阵”.如图2,用2×2的方框围住了其中的四个数,如果围住的这四个数中的某三个数的和是27,那么这三个数是a,b,c,d中的_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
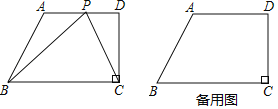
【题目】如图所示,在四边形ABCD中,AD∥BC,CD⊥BC,∠ABC=60°,且AD=12,BC=18.动点P从点A出发,以每秒2个单位长度的速度向点D运动,设运动时间为t秒(0<t≤6)
(1)当t=6时,cos∠BPC= ;
(2)当△BPC的外接圆与AD相切时,求t的值;
(3)在点P运动过程中,cos∠BPC是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
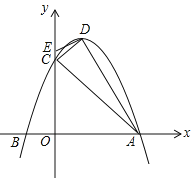
【题目】已知,抛物线![]() (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使![]() ,求点P的坐标;
,求点P的坐标;
(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx﹣c,它与x轴交于A、B,且A、B位于原点两侧,与y的正半轴交于C,顶点D在y轴右侧的直线l:y=4上,则下列说法:①bc<0;②0<b<4;③AB=4;④S△ABD=8.其中正确的结论有( )
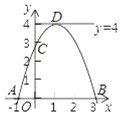
A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线![]() 经过C、B两点,与x轴的另一交点为D.
经过C、B两点,与x轴的另一交点为D.
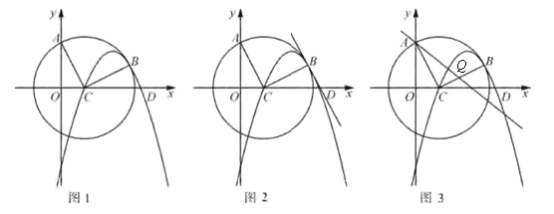
(1)点B的坐标为( , ),抛物线的表达式为 .
(2)如图2,求证:BD//AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com