
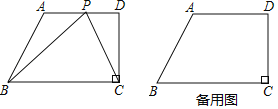
【题目】如图所示,在四边形ABCD中,AD∥BC,CD⊥BC,∠ABC=60°,且AD=12,BC=18.动点P从点A出发,以每秒2个单位长度的速度向点D运动,设运动时间为t秒(0<t≤6)
(1)当t=6时,cos∠BPC= ;
(2)当△BPC的外接圆与AD相切时,求t的值;
(3)在点P运动过程中,cos∠BPC是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)过点A作AM⊥BC于M,证四边形AMCD为矩形,在Rt△ABM中求出AM的长度,推出CD的长度,在Rt△BDC中求出cos∠BDC的值即可;
(2)作BC的中垂线PH交BC于点H,交AD于点P',连接BP',CP',作△BP'C的外接圆⊙O,则当点P运动到P'时,∴O与AD相切,求出此时t的值即可;
(3)连接PB,PC,设PB交⊙O于点N,连接NC,OB,先证明当动点P处于P’处时,∠BPC最大,则cos∠BPC的值最小,再证明∠BOH=∠BP'C,求出此时cos∠BP'C的值即可.
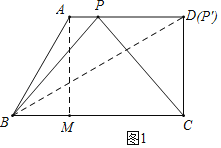
解:(1)如图1,过点A作AM⊥BC于M,
∵CD⊥BC,
∴∠DCB=∠AMC=90°,
∵AD∥BC,
∴∠D=180°﹣90°=90°,
∴四边形AMCD为矩形,
∴AD=MC=12,
∴BM=BC﹣MC=6,
在Rt△ABM中,BM=6,∠ABC=60°,
∴AM=![]() BM=6
BM=6![]() ,
,
∴CD=AM=6![]() ,
,
当t=6时,AP=2t=12,
∴点P与点D重合,
如图1,在Rt△BP'C中,P'C=6![]() ,BC=18,
,BC=18,
∴BP'=![]() =12
=12![]() ,
,
∴cos∠BP'C=![]() =
=![]() ;
;
故答案为:![]() ;
;
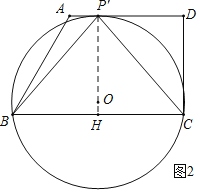
(2)如图2,作BC的中垂线PH交BC于点H,交AD于点P',连接BP',CP',作△BP'C的外接圆⊙O,
则P'B=P'C,圆心O在直线P'H上,
又∵AD∥BC,
∴P'H⊥AD,
∴当点P运动到P'时,∴O与AD相切,
∴∠DP'H=∠P'HC=∠HCD=90°,
∴四边形P'HCD为矩形,
∴P'D=HC=![]() BC=9,
BC=9,
则AP'=AD﹣P'D=12﹣9=3,
∴t=![]() ,
,
∴当△BPC的外接圆与AD相切时,t=![]() ;
;
(3)存在,
如图3,由(2)知,
当t=![]() 秒时,△BPC的外接圆OO与AD相切于点P’
秒时,△BPC的外接圆OO与AD相切于点P’
∵P'H=DC=6![]() >
>![]() BC=9,
BC=9,
∴P'H>BH,
∴∠BP'C<90°,圆心O在弦BC的上方,P是AD上一动点,
连接PB,PC,设PB交⊙O于点N,连接NC,
则∠BP'C=∠BNC≥∠BPC,
∴当动点P处于P’处时,∠BPC最大,则cos∠BPC的值最小,
此时,连接OB,则∠BOH=2∠BP'H=∠BP'C,
由题意,知OB=OP'=P'H﹣OH=6![]() ﹣OH,
﹣OH,
在Rt△BOH中,OH2+BH2=OB2,
∴OH2+92=(6![]() ﹣OH)2,
﹣OH)2,
解得,OH=![]() ,
,
∴OB=6![]() ﹣OH=
﹣OH=![]() ,
,
在Rt△BOH中,
cos∠BOH=![]() =
=![]() ,
,
∵∠BOH=∠BP'C,
∴cos∠BPC的值最小为![]() .
.



 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,求证四边形FFG是平行四边形.根据以下思路可以证明四边形EFGH是平行四边形:
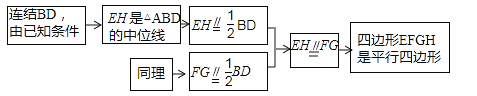
(1)根据上述思路,请你写出完整的证明过程;
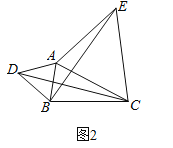
(2)如图,已知![]() ,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BF.可通过证明△________≌△________,得到
,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BF.可通过证明△________≌△________,得到![]() ;
;
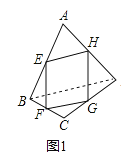
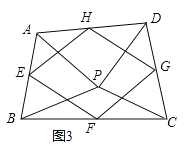
(3)如图③,点P是四边形ABCD内一点,且满足![]() ,
,![]() ,
,![]() ,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明.
,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到数字“﹣1”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的操作规则
第一次操作:对任意相邻的两个数,都用左边的数减去右边的数,所得的差写在这两个数之间,得到一组依次排列的新数串;第二次操作:对上一次操作得到的新数串,仍按照第一次操作进行,又得到一组依次排列的新数串;……这样依次操作下去
(1)对依次排列的3个数:﹣2,3,6,按上面的规则进行操作,
①齐第一次操作后得到的新数串:﹣2, ,3, ,6此次增加的新数之和为 ;
②出第二次操作后得到的新数中,并求第二次操作后再次增加的新数之和;
(2)对依次排列的3个数:1,3,﹣![]() ,按上述规则操作,直接写出第三次操作后再次增加的新数之和是 .
,按上述规则操作,直接写出第三次操作后再次增加的新数之和是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
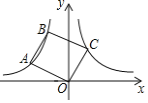
【题目】如图,点A、B在双曲线![]() (x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线
(x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线![]() (x>0)上,此时OABC的面积为( ).
(x>0)上,此时OABC的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
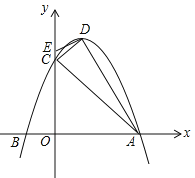
【题目】已知,抛物线![]() (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使![]() ,求点P的坐标;
,求点P的坐标;
(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
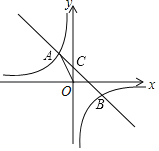
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() (k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=
(k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=![]() .
.
(1)求k的值;
(2)直接写出点B的坐标,并求直线AB的解析式;
(3)P是y轴上一点,且S△PBC=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王同学使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为![]() ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com