
����Ŀ���Ķ�����IJ�������
��һ�β��������������ڵ���������������ߵ�����ȥ�ұߵ��������õIJ�д����������֮�䣬�õ�һ���������е����������ڶ��β���������һ�β����õ��������������յ�һ�β������У��ֵõ�һ���������е��������������������β�����ȥ
��1�����������е�3��������2��3��6��������Ĺ�����в�����
�����һ�β�����õ�������������2���� ����3���� ����6�˴����ӵ�����֮��Ϊ�� ����
�ڳ��ڶ��β�����õ��������У�����ڶ��β������ٴ����ӵ�����֮�ͣ�
��2�����������е�3������1��3����![]() �����������������ֱ��д�������β������ٴ����ӵ�����֮������ ����
�����������������ֱ��д�������β������ٴ����ӵ�����֮������ ����
���𰸡���1����-5��-3��-8����-8����2��![]()
��������
������ߵ�����ȥ�ұߵ��������õIJ�д����������֮�䣬�õ�һ���������е���������Ȼ����㼴�ɣ�
�⣺��1���٩�2��3����5��3��6����3��
����5��+����3������8��
�ʴ�Ϊ��5����3����8��
�ڵڶ��β�����õ�����������
��2��3����5����8��3��6����3����9��6��
�ڶ��β������ٴ����ӵ�����֮����3+����8��+6+����9������8��
��2����һ�β�����õ����������ǣ�1����2��3��![]() ����
����![]()
�ڶ��β�����õ����������ǣ�1��3����2����5��3����![]() ��
��![]() ��4����
��4����![]() ��
��
�����β�����õ����������ǣ�1����2��3��5����2��3����5����8��3��![]() ����
����![]() ����4��
����4��![]() ��
��![]() ��4��
��4��![]() ����
����![]() ��
��
��2+5+3+����8��+![]() +����4��+����
+����4��+����![]() ��+��
��+��![]() ����
����![]() ��
��
�ʴ�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=3��AC=4��BC=5��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F��MΪEF�е㣬��AM����СֵΪ��( )
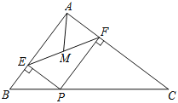
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD��AB=4��BC=3����P��BC���ϣ�����CDP��DP�۵�����C���ڵ�E����PE��DE�ֱ�AB�ڵ�O��F����OP=OF����cos��ADF��ֵΪ��������
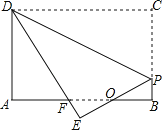
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��y����![]() x+6�ֱ���x�ᡢy�ύ�ڵ�A��B������P���߶�AB����P����A��B�غϣ����˶�ʱ��������ϵ�ڴ���һ��N��ʹ����O��B��P��NΪ������ı���Ϊ���Σ���ֱ��д��N������_____��
x+6�ֱ���x�ᡢy�ύ�ڵ�A��B������P���߶�AB����P����A��B�غϣ����˶�ʱ��������ϵ�ڴ���һ��N��ʹ����O��B��P��NΪ������ı���Ϊ���Σ���ֱ��д��N������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������أ���������ϱ�����������ţ�������һʮ������ľ���ʣ������ż��β�����ľ������λ�ժ�ԡ���������������˼��˵����ͼ�����γdz�ABCD�����߳�ǽAB��9��ϱ߳�ǽAD��7����ŵ�E�����ŵ�F�ֱ���AB��AD�е㣬EG��AB��FH��AD��EG��15�HG����A�㣬��FH���� ��

A.1.2 ��B.1.5 ��C.1.05 ��D.1.02 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����ı���ABCD�У�AD��BC��CD��BC����ABC��60�㣬��AD��12��BC��18������P�ӵ�A��������ÿ��2����λ���ȵ��ٶ����D�˶������˶�ʱ��Ϊt�루0��t��6��
��1����t��6ʱ��cos��BPC���� ����
��2������BPC�����Բ��AD����ʱ����t��ֵ��
��3���ڵ�P�˶������У�cos��BPC�Ƿ������Сֵ�������ڣ�����������Сֵ���������ڣ���˵�����ɣ�
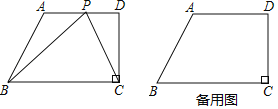
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=![]() ����A=120�㣬��P��Q��K�ֱ�Ϊ�߶�BC��CD��BD�ϵ�����һ�㣬��PK+QK����СֵΪ____________��
����A=120�㣬��P��Q��K�ֱ�Ϊ�߶�BC��CD��BD�ϵ�����һ�㣬��PK+QK����СֵΪ____________��
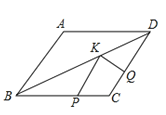
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�OAB�У���AOB��90�㣬AO��2��BO��4������OAB�ƶ���O��˳ʱ�뷽����ת����OA1B1������ʱ�߶�OB1��AB�Ľ���Dǡ��Ϊ�߶�AB���е㣬�߶�A1B1��OA���ڵ�E����ͼ����Ӱ���ֵ����__��
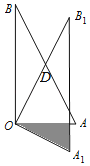
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O ����ABC �����Բ��O ���� BC ���ϣ���BAC ��ƽ���߽���O �ڵ� D������ BD��CD������ D �� BC ��ƽ���ߣ��� AB ���ӳ����ཻ�ڵ� P��
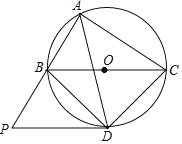
��1����֤��PD ����O �����ߣ�
��2����֤����PBD�ס�DCA��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com