
【题目】如图,在菱形ABCD中,AB=![]() ,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为____________.
,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为____________.
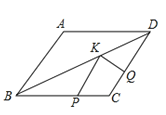
【答案】6
【解析】
根据菱形的对称性,在AB上找到点P关于BD的对称点![]() ,过点
,过点![]() 作
作![]() Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E,根据垂线段最短和平行线之间的距离处处相等,可得此时
Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E,根据垂线段最短和平行线之间的距离处处相等,可得此时![]() 最小,且最小值为
最小,且最小值为![]() 的长,
的长,![]() ,然后利用锐角三角函数求AE即可.
,然后利用锐角三角函数求AE即可.
解:根据菱形的对称性,在AB上找到点P关于BD的对称点![]() ,过点
,过点![]() 作
作![]() Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E
Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E
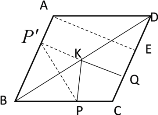
根据对称性可知:PK=![]() K,
K,
∴此时![]() =
=![]() ,根据垂线段最短和平行线之间的距离处处相等,
,根据垂线段最短和平行线之间的距离处处相等,
∴此时![]() 最小,且最小值为
最小,且最小值为![]() 的长,
的长,![]()
∵在菱形![]() 中,
中,![]() ,
,![]()
∴![]() ,∠ADE=180°-∠A=60°
,∠ADE=180°-∠A=60°
在Rt△ADE中,AE=AD·sin∠ADE=![]()
∴![]()
即![]() 的最小值为6
的最小值为6
故答案为6.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )
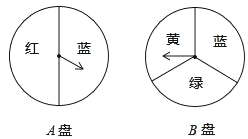
A. 两个转盘转出蓝色的概率一样大
B. 如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C. 先转动A 转盘再转动B 转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D. 游戏者配成紫色的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的操作规则
第一次操作:对任意相邻的两个数,都用左边的数减去右边的数,所得的差写在这两个数之间,得到一组依次排列的新数串;第二次操作:对上一次操作得到的新数串,仍按照第一次操作进行,又得到一组依次排列的新数串;……这样依次操作下去
(1)对依次排列的3个数:﹣2,3,6,按上面的规则进行操作,
①齐第一次操作后得到的新数串:﹣2, ,3, ,6此次增加的新数之和为 ;
②出第二次操作后得到的新数中,并求第二次操作后再次增加的新数之和;
(2)对依次排列的3个数:1,3,﹣![]() ,按上述规则操作,直接写出第三次操作后再次增加的新数之和是 .
,按上述规则操作,直接写出第三次操作后再次增加的新数之和是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(1,2)、B(3,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
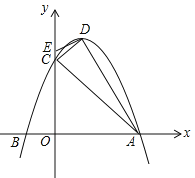
【题目】已知,抛物线![]() (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使![]() ,求点P的坐标;
,求点P的坐标;
(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营A种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量.
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付仓库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,依此方式,绕点
,依此方式,绕点![]() 连续旋转2019次得到正方形
连续旋转2019次得到正方形![]() ,如果点
,如果点![]() 的坐标为(1,0),那么点
的坐标为(1,0),那么点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com