
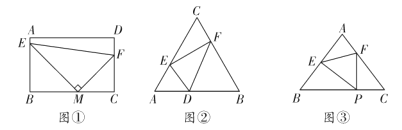
����Ŀ����1����һ����ѧ̽�����ϣ�ѧ���Ƿ�����һ�����ɣ�
��ͼ�٣����ı���![]() �Ǿ���ʱ��
�Ǿ���ʱ��![]() ��ֱ�Ƕ���M��
��ֱ�Ƕ���M��![]() �����˶���ֱ�DZ߷ֱ����߶�
�����˶���ֱ�DZ߷ֱ����߶�![]() ���߶�
���߶�![]() ����E��F���㣬�ڵ�M�˶��Ĺ����У�ʼ�մ�����
����E��F���㣬�ڵ�M�˶��Ĺ����У�ʼ�մ�����![]() .��������ͬѧ��������⣬������ı��λ���������ʱ���Ƿ��Դ���ͬ���Ĺ����أ���ͼ�ڣ���
.��������ͬѧ��������⣬������ı��λ���������ʱ���Ƿ��Դ���ͬ���Ĺ����أ���ͼ�ڣ���![]() �У�
�У�![]() ����DΪ
����DΪ![]() ���ϵĶ��㣬����D��
���ϵĶ��㣬����D��![]() ����
����![]() �ڵ�E����
�ڵ�E����![]() �ڵ�F�������Ƿ�����������Ƶ������Σ������ڣ���֤�����������ڣ���˵�����ɣ�
�ڵ�F�������Ƿ�����������Ƶ������Σ������ڣ���֤�����������ڣ���˵�����ɣ�
��2������������ɣ�����������⣺
��ͼ�ۣ���![]() �У�
��![]() ��
��![]() ����PΪ
����PΪ![]() ��һ�㣨����B��C�غϣ�������P��
��һ�㣨����B��C�غϣ�������P��![]() �ڵ�E��
�ڵ�E��![]() ��
��![]() �ڵ�F����
�ڵ�F����![]() Ϊ���������Σ���
������������![]() �ij�.
�ij�.
���𰸡���1�������������Ƶ������Σ�![]() ��֤�������������2��
��֤�������������2��![]() �ij�Ϊ
�ij�Ϊ![]() ��
��![]() ��2.
��2.
��������
��1����![]() ��
��![]() ��
��![]() ����
����![]() ���Ӷ�֤��
���Ӷ�֤��![]() ��
��![]() ���ƣ�
���ƣ�
��2����֤![]() ����
����![]() Ϊ����������ʱ����
Ϊ����������ʱ����![]() ��
��![]() ����������ۣ��ֱ����
����������ۣ��ֱ����![]() �ij�������.
�ij�������.
��1�������������Ƶ������Σ�![]() ���������£�
���������£�
��![]() ��
��![]() ��
�У�
��![]() ��
��
![]() ��
��
��![]() .
.
�֡�![]() ��
��
��![]() .
.
��![]() ��
��
��2����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
�֡�![]() ��
��
��![]() ��
��
��![]() .
.
��![]() ������������
Ϊ���������Σ���![]() ���ɷ���������������ۣ�
���ɷ���������������ۣ�
�ٵ�![]() ʱ����
ʱ����![]() ��
��
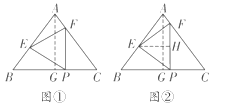
��![]() ����ͼ�٣�����A��
����ͼ�٣�����A��![]() ��
��![]() �ڵ�G��
�ڵ�G��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����ã�
����ã�![]() ��
��
�ڵ�![]() ʱ����ͼ�ڣ�����A��
ʱ����ͼ�ڣ�����A��![]() �ڵ�G������E��
�ڵ�G������E��![]() ��
��![]() �ڵ�H����
�ڵ�H����![]() .
.
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() .
.
��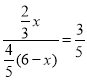 ����ã�
����ã�![]() ��
��
�۵�![]() ʱ����ͼ�ۣ�����F��
ʱ����ͼ�ۣ�����F��![]() ��
��![]() �ڵ�M��
�ڵ�M��
![]() ��
��
![]() ��
��
��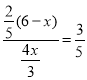 ����ã�
����ã�![]() .
.
����������![]() �ij�Ϊ
�ij�Ϊ![]() ��
��![]() ��2.
��2.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
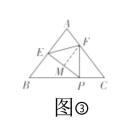
����Ŀ����ͼ������ABC��BC���ϵ�����ADƽ�Ƶ���A'B'C'��λ�ã���֪��ABC�����Ϊ9����Ӱ���������ε����Ϊ4����AA'=1����A'D���ڣ�������

A. 2 B. 3 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����
����![]() ��
��![]() ��
��![]() �DZ�
�DZ�![]() ������һ��(��
������һ��(��![]() ���
���![]() ��
��![]() ���غ�)����
���غ�)����![]() Ϊһֱ�DZ���
Ϊһֱ�DZ���![]() ���ⲿ��
���ⲿ��![]() ��
��![]() ������
������![]() ��
��![]() ��
��
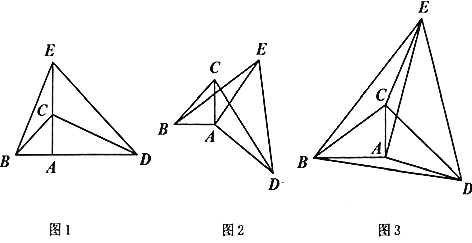
��1����ͼ![]() �У���
����![]() ��
��![]() ���ֽ�ͼ
���ֽ�ͼ![]() �е�
�е�![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת���
˳ʱ����ת���![]() ���õ�ͼ
���õ�ͼ![]() ����ô�߶�
����ô�߶�![]() ��
��![]() ֮���������Ĺ�ϵ��д�����ۣ���˵�����ɣ�
֮���������Ĺ�ϵ��д�����ۣ���˵�����ɣ�
��2����ͼ![]() �У���
����![]() ��
��![]() ��
��![]() ��
��![]() ���ֽ�ͼ
���ֽ�ͼ![]() �е�
�е�![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת���
˳ʱ����ת���![]() ���õ�ͼ
���õ�ͼ![]() ������
������![]() ��
��![]() ��
��
����֤��![]() ��
��
�ڼ��㣺![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ������ֽ�е���ѧ
���ⱳ��
����ѧ����ϣ���ʦ���Ƚ�ƽ���ı���ֽƬABCD����ͼ����ʾ��ʽ�۵���ʹ��C���A�غϣ���D�䵽D�䴦���ۺ�ΪEF����ʱͬѧ�Ǻܿ�֤�ã���AEF�ǵ��������Σ���������ѧϰС��Ҳ���ֲ���������������������������⣮
��������
(1) �����ȡ�С�齫����ֽƬABCD��������ʽ�۵�����ͼ�ڣ������ص����֡�AEFǡ���ǵȱ������Σ������ABCD�ij�����֮���Ƕ��٣�
ʵ��̽��
(2)����־��С�齫����ֽƬABCD��EF�۵�����ͼ�ۣ�ʹB������AD���ϵ�B�䴦����B��G�۵���ʹD������D�䴦����B��D���F�㣮��̽���ı���EFGB����ʲô�����ı��Σ�
(3)��̽������ͼ��������BB�䣬���жϲ�֤����BB��G����״��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ֱ�������֩�1��0��1��2�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯��ϴ���ȣ�
��1�������ȡһ�ſ�Ƭ����鵽���֡���1���ĸ��ʣ�
��2�������ȡһ�ſ�Ƭ��Ȼ�Żأ��������ȡһ�ſ�Ƭ�������б�����״ͼ�ķ��������һ�γ鵽���֡�2���ҵڶ��γ鵽���֡�0���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��l1��l2��l3��l4��l5����l1��l2��l3��l4��l5����������ֱ��֮��ľ�����ȣ���ABC�Ķ���A��B��C�ֱ���l1��l3��l5�ϣ�AB��l2�ڵ�D��BC��l4�ڵ�E��AC��l2�ڵ�F������DEF�������1�����ABC������ǣ�������
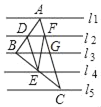
A.3. 5B.4C.4.5D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=��x2+mx+n��x���ڵ�A����2��0���͵�B����y���ڵ�C��0��2����
��1���������ߵĺ�������ʽ��
��2������M���������ϣ���S��AOM=2S��BOC�����M�����ꣻ
��3����ͼ2�����N���߶�AC�ϵ�һ���㣬��DN��x�ᣬ���������ڵ�D�����߶�DN���ȵ����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
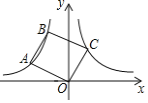
����Ŀ����ͼ����A��B��˫����![]() ��x��0���ϣ�����OA��AB����OA��ABΪ����OABC������Cǡ����˫����
��x��0���ϣ�����OA��AB����OA��ABΪ����OABC������Cǡ����˫����![]() ��x��0���ϣ���ʱOABC�����Ϊ����������
��x��0���ϣ���ʱOABC�����Ϊ����������
A.![]() B.
B.![]() C.
C.![]() D.4
D.4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������Ƴ����ڸ���������������������Ҫ��30�����ڽ��壬��������Ϣ���������ڻ�ڼ乺���˼۸�Ϊ12��Ԫ�����������������ƽ��ÿ�¸���![]() ��Ԫ��
��Ԫ��![]() ���½��壮
���½��壮![]() ��
��![]() �ĺ�����ϵ��ͼ��ʾ������ͼ��ش��������⣺
�ĺ�����ϵ��ͼ��ʾ������ͼ��ش��������⣺
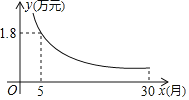
��1��ȷ��![]() ��
��![]() �ĺ�������ʽ��������������Ŀ��
�ĺ�������ʽ��������������Ŀ��
��2������������20���½��壬ƽ��ÿ��Ӧ��������Ԫ��
��3���������ÿ�¸������4000Ԫ������������Ҫ�����²��ܽ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com