
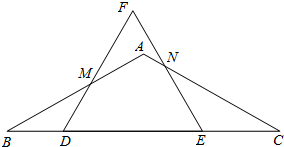
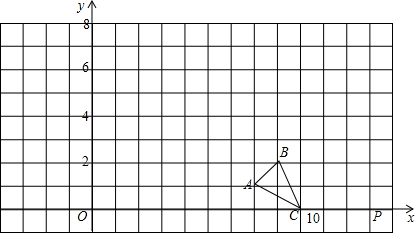
分析 (1)由AB=AC,∠B=30°,根据等边对等角,可求得∠C=∠B=30°,又由△DEF是等边三角形,根据等边三角形的性质,易求得∠MDB=∠NEC=120°,∠BMD=∠B=∠C=∠CNE=30°,即可判定:△BMD∽△CNE;
(2)首先过点M作MH⊥BC,设BD=x,由以M为圆心,以MF为半径的圆与BC相切,可得MH=MF=4-x,由(1)可得MD=BD,然后在Rt△DMH中,利用正弦函数,即可求得答案;
(3)过M作EF的垂线MG,那么MG=BM,可在三角形BDM中用BD来表示出BM,因为BD=DM,所以可以用BD表示出FM,进而在直角三角形FMG中表示出MG,然后让这两个含x的式子相等即可求出x的值;
(4)首先求得△ABC的面积,继而求得△BDM的面积,然后由相似三角形的性质,可求得△CNE的面积,再利用二次函数的最值问题,即可求得答案.
解答 (1)证明:∵AB=AC,
∴∠B=∠C=30°,
∵△DEF是等边三角形,
∴∠FDE=∠FED=60°,
∴∠MDB=∠NEC=120°,
∴∠BMD=∠B=∠C=∠CNE=30°,
∴△BMD∽△CNE;
(2)解:如图1,过点M作MH⊥BC,
∵以M为圆心,以MH为半径的圆,则与BC相切,
∴MH=MF,
设BD=x,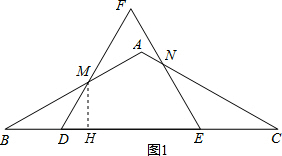
∵△DEF是等边三角形,
∴∠FDE=60°,
∵∠B=30°,
∴∠BMD=∠FDE-∠B=60°-30°=30°=∠B,
∴DM=BD=x,
∴MH=MF=DF-MD=4-x,
在Rt△DMH中,sin∠MDH=sin60°=$\frac{MH}{MD}$=$\frac{4-x}{x}$=$\frac{\sqrt{3}}{2}$,
解得:x=16-8$\sqrt{3}$,
∴当BD=16-8$\sqrt{3}$时,以M为圆心,以MF为半径的圆与BC相切;
(3)如图2,过点M作MG⊥EF垂足为G,则MG=BM,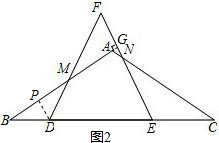
在△BDM中,过点D作DP⊥BM垂足为P,
∵BD=x,∠B=30°,
∴BP=$\frac{\sqrt{3}}{2}$,BM=$\sqrt{3}$.
∵BD=DM,FD=DE=4,
∴FM=4-x.
∵在RT△FMG中,∠F=60°,
∴MG=$\frac{\sqrt{3}(4-x)}{2}$.
∴$\sqrt{3}$x=$\frac{\sqrt{3}(4-x)}{2}$.
解得x=$\frac{4}{3}$.
所以当BD的长为$\frac{4}{3}$时,以M为圆心,BM为半径的圆与直线EF相切.
(4)解:如图3,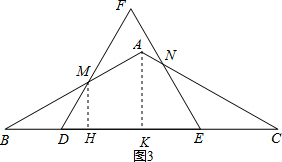 过点M作MH⊥BC于H,过点A作AK⊥BC于K,
过点M作MH⊥BC于H,过点A作AK⊥BC于K,
∵AB=AC,
∴BK=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∵∠B=30°,
∴AK=BK•tan∠B=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴S△ABC=$\frac{1}{2}$BC•AK=$\frac{1}{2}$×8×$\frac{4\sqrt{3}}{3}$=$\frac{16\sqrt{3}}{3}$,
由(2)得:MD=BD=x,
∴MH=MD•sin∠MDH=$\frac{\sqrt{3}}{2}$x,
∴S△BDM=$\frac{1}{2}$•x•$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{4}$x2,
∵△DEF是等边三角形且DE=4,BC=8,
∴EC=BC-BD-DE=8-x-4=4-x,
∵△BMD∽△CNE,
∴S△BDM:S△CEN=($\frac{BD}{CE}$)2=$\frac{{x}^{2}}{(4-x)^{2}}$,
∴S△CEN=$\frac{\sqrt{3}}{4}$(4-x)2,
∴y=S△ABC-S△CEN-S△BDM=$\frac{16\sqrt{3}}{3}$-$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{4}$(4-x)2=-$\frac{\sqrt{3}}{2}$x2+2$\sqrt{3}$x+$\frac{4\sqrt{3}}{3}$=-$\frac{\sqrt{3}}{2}$(x-2)2+$\frac{10\sqrt{3}}{3}$($\frac{4}{3}$<x<$\frac{8}{3}$),
当x=2时,y有最大值,最大值为$\frac{10\sqrt{3}}{3}$.
点评 此题考查了相似三角形的判定与性质、等腰三角形的性质、等边三角形的性质、二次函数的性质以及三角函数等知识.此题综合性较强,难度较大,注意数形结合思想与方程思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
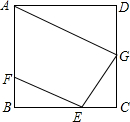 如图,正方形ABCD中,AB=1,G为DC的中点,E为BC上任意一点,(点E与B,C不重合)过E作GA的平行线交AB于F.设BE=x,四边形AFEG面积为y,试写出y关于x的函数关系式,并指出自变量x的取值范围.
如图,正方形ABCD中,AB=1,G为DC的中点,E为BC上任意一点,(点E与B,C不重合)过E作GA的平行线交AB于F.设BE=x,四边形AFEG面积为y,试写出y关于x的函数关系式,并指出自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com