
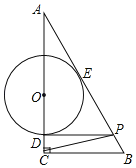
【题目】如图,在Rt△ABC中,∠C=90°,点O在边AC上,⊙O与边AC相交于点D、与边AB相切于点E,过点D作DP∥BC交AB于点P.
(1)求证:PD=PE;
(2)连接CP,若点E是AP的中点,OD:DC=2:1,CP=13,求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为2![]()
【解析】
(1)先由平行线的性质和圆的切线的判定定理得出PD是⊙O的切线,再根据切线长定理即可证;
(2)如图(见解析),连接OE、DE,利用直角三角形斜边中线的性质和题(1)的结论可得![]() 是等边三角形,再利用直角三角形两锐角互余可得
是等边三角形,再利用直角三角形两锐角互余可得![]() 的度数,然后利用三角函数可得半径与AE的等量关系,从而可知半径与PD的等量关系,最后在
的度数,然后利用三角函数可得半径与AE的等量关系,从而可知半径与PD的等量关系,最后在![]() 中利用勾股定理求出DC的长,从而可得圆的半径.
中利用勾股定理求出DC的长,从而可得圆的半径.
(1)![]()
![]()
![]()
![]() 是⊙O的半径
是⊙O的半径
∴PD是⊙O的切线
∵PE是⊙O的切线
![]() ;
;
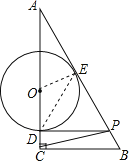
(2)如图,连接OE、DE
∵点E是AP的中点,且![]() 是直角三角形
是直角三角形
![]()
![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
![]()
∵PE与⊙O切点E
![]()
![]()
∴设![]() ,则
,则![]()
在![]() 中,
中,![]()
则![]()
![]()
在![]() 中,
中,![]()
![]() ,解得
,解得![]()
![]()
故⊙O的半径为![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
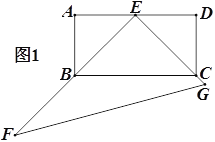
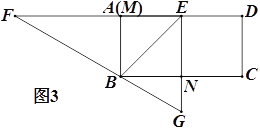
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
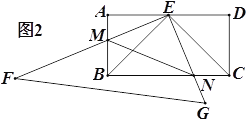
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形ABCO的点B坐标(3,3),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.若点D坐标为(2,0),则点E坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
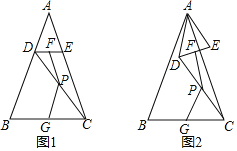
【题目】如图1,在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,连接DC,点F、P、G分别为DE、DC、BC的中点.
(1)观察猜想:图1中,线段PF与PG的数量关系是 ,∠FPG= (用含α的代数式表示)
(2)探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出PF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
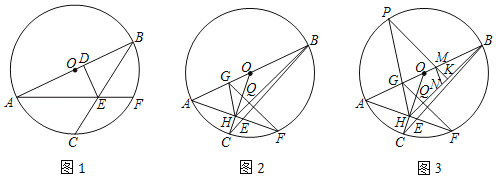
【题目】已知,AB为⊙O的直径,弦BC、AF相交于点E,过点E作ED⊥AB,∠AEC=∠BED.
(1)如图1,求证:![]() ;
;
(2)如图2,当∠BAF=45°时,OC交AF于点H,作FG⊥BH于点Q,交AB于点G,连接GH,求证:∠AGH=∠BGF;
(3)如图3,在(2)的条件下,射线HG与⊙O交于点P,过点P作PK⊥BH交AB于点M,垂足为点K,点N为BH的中点,MN=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“生成三角形”.
(1)已知点A(4,0);
①若以线段OA为底的某等腰三角形恰好是点O,A的“生成三角形”,求该三角形的腰长;
②若Rt△ABC是点A,B的“生成三角形”,且点B在x轴上,点C在直线y=2x﹣5上,则点B的坐标为 ;
(2)⊙T的圆心为点T(2,0),半径为2,点M的坐标为(2,6),N为直线y=x+4上一点,若存在Rt△MND,是点M,N的“生成三角形”,且边ND与⊙T有公共点,直接写出点N的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,卧龙中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____度;
(2)请补全条形统计图;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
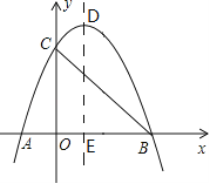
【题目】如图,抛物线![]() 与x轴交于点A(-1,0),B(3,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴与点E,则下列结论:①2a+b=0;②b+2c>0;③a+b>am
与x轴交于点A(-1,0),B(3,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴与点E,则下列结论:①2a+b=0;②b+2c>0;③a+b>am![]() +bm(m为任意实数);④一元二次方程
+bm(m为任意实数);④一元二次方程![]() 有两个不相等的实数根;⑤当△BCD为直角三角形时,a的值有2个;⑥若点P为对称轴上的动点,则
有两个不相等的实数根;⑤当△BCD为直角三角形时,a的值有2个;⑥若点P为对称轴上的动点,则![]() 有最大值,最大值为
有最大值,最大值为![]() .其中正确的有( )
.其中正确的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步
是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步![]() 小路的宽度不计
小路的宽度不计![]() 观测得点B在点A的南偏东
观测得点B在点A的南偏东![]() 方向上,点C在点A的南偏东
方向上,点C在点A的南偏东![]() 的方向上,点B在点C的北偏西
的方向上,点B在点C的北偏西![]() 方向上,AC间距离为400米
方向上,AC间距离为400米![]() 问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
![]() 参考数据:
参考数据:![]() ,
,![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com