
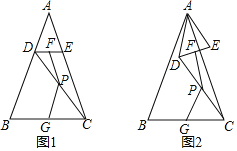
【题目】如图1,在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,连接DC,点F、P、G分别为DE、DC、BC的中点.
(1)观察猜想:图1中,线段PF与PG的数量关系是 ,∠FPG= (用含α的代数式表示)
(2)探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出PF的最大值.
【答案】(1)PF=PG,180°﹣α;(2)∠FPG=180°﹣α;证明见解析;(3)PF的最大值为4.
【解析】
(1)根据等腰三角形的性质和三角形的中位线定理解答即可;
(2)连接BD,CE,利用全等三角形的判定和性质以及三角形中位线定理解答;
(3)当EC最大时,FP最大,进而解答即可.
(1)如图1,∵在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,
∴AB﹣AD=AC﹣AE,
即DB=CE,
∵点F、P、G分别为DE、DC、BC的中点,
∴PF=![]() CE,PG=
CE,PG=![]() BD,
BD,
∴PF=PG,
∵点F、P、G分别为DE、DC、BC的中点,
∴PG∥BD,PF∥CE,
∴∠PGC=∠DBC,∠DPF=∠DCE,
∴∠FPG=∠DPF+∠DPG
=∠DCE+∠PGC+∠DCB
=∠ACD+∠ACE+∠DBC+∠DCB
=∠ACD+∠ABD+∠DBC+∠DCB
=∠ABC+∠ACB,
∵∠ABC+∠ACB=180°﹣∠BAC
∴∠FPG=180°﹣α;
故答案为PF=PG,180°﹣α;
(2)如图2,连接BD,CE,由题意知AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点F、P、G分别为DE、DC、BC的中点,
∴PF,PG分别是△CDE和△CDB的中位线,
∴PG∥BD,PF∥CE,
∴∠PGC=∠DBC,∠DPF=∠DCE,
∴∠FPG=∠DPF+∠DPG
=∠DCE+∠PGC+∠DCB
=∠ACD+∠ACE+∠DBC+∠DCB
=∠ACD+∠ABD+∠DBC+∠DCB
=∠ABC+∠ACB,
∵∠ABC+∠ACB=180°﹣∠BAC
∴∠FPG=180°﹣α;
(3)当EC最大时,FP最大,EC的最大值为AE+AC=8,
∴PF=![]() EC,即PF的最大值为4.
EC,即PF的最大值为4.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,点E为AC延长线上一点,连接DE,过点D作DF⊥DE交CB的延长线于点F.
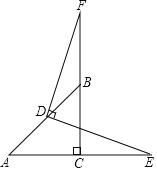
(1)求证:BF=CE;
(2)若CE=AC,用等式表示线段DF与AB的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A,C(1,0),与y轴交于点B(0,﹣3).
(1)求抛物线的解析式;
(2)点P是直线AB下方的抛物线上一动点,过点P作x轴的垂线,垂足为点F,交直线AB于点E,作PD⊥AB于点D.当△PDE的周长最大时,求出点P的坐标.
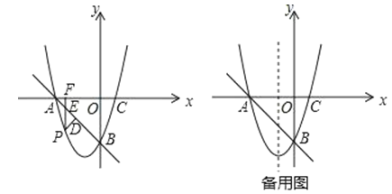
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
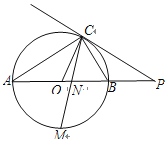
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
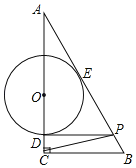
【题目】如图,在Rt△ABC中,∠C=90°,点O在边AC上,⊙O与边AC相交于点D、与边AB相切于点E,过点D作DP∥BC交AB于点P.
(1)求证:PD=PE;
(2)连接CP,若点E是AP的中点,OD:DC=2:1,CP=13,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着襄阳市近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图1所示;种植花卉的利润
成正比例关系,如图1所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
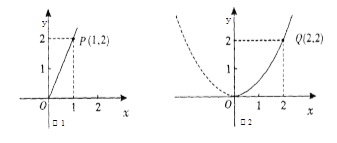
(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以10万元资金投入种植花卉和树木,求他获得的最大利润是多少?
(3)在(2)的条件下,根据对市场需求的调查,这位专业户决定投入种植树木的资金不得高于投入种植花卉的资金,他至少获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有
“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.
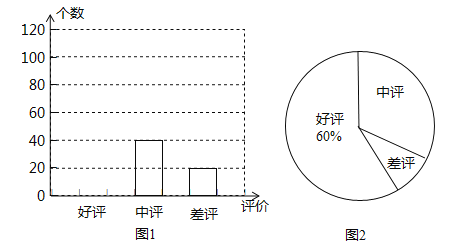
(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com