
【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

【答案】(1)见解析;(2)α,β之间的数量关系式为2α+β=60°.
【解析】
(1)根据三角形的中位线的性质得到EF=![]() CD,根据直角三角形的性质得到AE=
CD,根据直角三角形的性质得到AE=![]() BD,于是得到结论;
BD,于是得到结论;
(2)根据题意得到△AEF是等边三角形,求得∠AEF=60°,根据三角形中位线的性质和三角形外角的性质即可得到结论.
(1)∵点E、F分别为DB、BC的中点,
∴EF=![]() CD,
CD,
∵∠DAB=90°,
∴AE=![]() BD,
BD,
∵DB=DC,
∴AE=EF;
(2)∵AF=AE,AE=EF,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵∠DAB=90°,点E、F分别为DB、BC的中点,
∴AE=DE,EF∥CD,
∴∠ADE=∠DAE=α,∠BEF=∠BDC=β,
∴∠AEB=2∠ADE=2α,
∴∠AEF=∠AEB+∠FEB=2α+β=60°,
∴α,β之间的数量关系式为2α+β=60°.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如下几个图形是五角星和它的变形.

(1)图甲是一个五角星 ABCDE,则∠A+∠B+∠C+∠D+∠E 的度数为 ;(不必 写过程)
(2)如图乙,如果点 B 向右移动到 AC 上时,则∠A+∠EBD+∠C+∠D+∠E 度数为 ;(不必写过程)
(3)如图丙,点 B 向右移动到 AC 的另一侧时,(1)的结论成立吗?为什么?
(4)如图丁,点 B,E 移动到∠CAD 的内部时,结论又如何?(不必写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
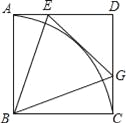
【题目】已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作![]() ,连结BG.
,连结BG.
(1)求证:EG与![]() 相切.
相切.
(2)求∠EBG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
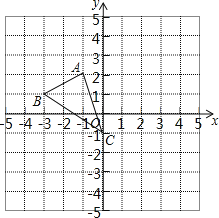
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
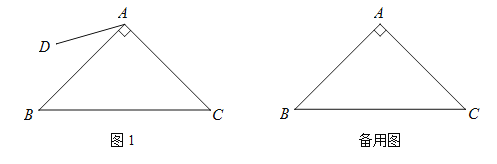
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com