
【题目】在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,点E为AC延长线上一点,连接DE,过点D作DF⊥DE交CB的延长线于点F.
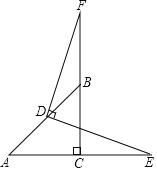
(1)求证:BF=CE;
(2)若CE=AC,用等式表示线段DF与AB的数量关系,并证明.
【答案】(1)详见解析;(2)DF![]() AB.
AB.
【解析】
(1)连接DC,由等腰直角△ABC的中线得CD=BD;等腰直角△ABC顶角平分线和底角,∠ABC与∠ABF互为邻补角,由∠BCE=90°,∠DCB=45°,计算出∠DBF=∠DCB=135°;∠CHE+∠E=90°;∠CHE=∠DHF等量代换得∠F=∠E,从而证明△DBF≌△DCE,最后根据全等三角形的性质求BF=CE.
(2)连接BE,在△DCE中,点D和C分别是AB和AE的中点,得到DC∥BE,在(1)基础上易证∠ABE=90°,AB=BE.计算出线段DE的长度与线段AB的关系,即求出线段DF与线段AB的关系.
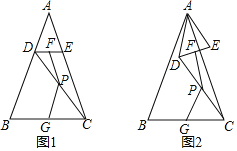
(1)连接CD,DE与CF相交于点H,如图1所示:

∵在Rt△ABC中,D为AB中点,
∴CD=BD,
又∵AC=BC,
∴DC⊥AB,
∴∠ABC=∠DCB=45°,
∵∠ACB=90°,
∴∠BCE=90°,
∵∠ABC+∠ABF=180°,∠DCE=∠DCB+∠BCE,
∴∠DBF=180°﹣45°=135°,∠DCB=90°+45°=135°,
∴∠DBF=∠DCB,
∵DF⊥DE,
∴∠DHF+∠F=90°,
又∵∠CHE+∠E=90°;∠CHE=∠DHF,
∴∠F=∠E,
在△DBF和△DCE中
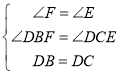 ,
,
∴△DBF≌△DCE(AAS),
∴BF=CE.
(2)线段DF与AB的数量关系:DF![]() AB.
AB.
连接BE,设AD=BD=a,则AB=2a.如图2所示

∵△DBF≌△DCE,
∴DF=DE.
∵CE=AC,DA=DB,
∴DC∥BE,
又∵∠ADC=90°,
∴∠ABE=90°,
∵∠A=45°,
∴∠AEB=45°,
∴AB=BE=2a,
在Rt△BDE中,由勾股定理得:
DE2=DB2+BE2,
∴DE![]() ,
,
∴DF![]() a,
a,
∴![]() .
.
即DF![]() AB.
AB.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
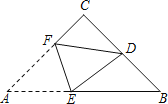
【题目】如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商经销的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份冰箱每台售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(y≤12),请问有几种进货方案?
(3)三月份为了促销,该经销商决定在二月份售价的基础上,每售出一台冰箱再返还顾客现金a元,而洗衣机按每台4400元销售,这种情况下,若(2)中各方案获得的利润相同,则a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
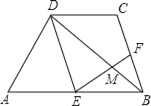
【题目】如图,AB∥CD,且AB=2CD,E是AB的中点,F是边BC上的动点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若F是BC的中点,BD=12,求BM的长;
(3)若AD=BC,BD平分∠ABC,点P是线段BD上的动点,是否存在点P使DPBP=BFCD,若存在,求出∠CPF的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在矩形 ABCD 中,AB=8,AD=10,E 是 CD 边上一点,连接 AE,将矩形 ABCD 沿 AE 折叠,顶点 D 恰好落在 BC 边上点 F 处,延长 AE 交 BC 的延长线于点G.
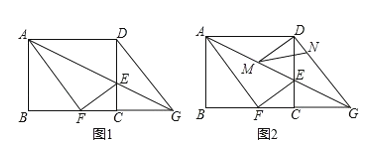
(1)求线段 CE 的长;
(2)如图 2,M,N 分别是线段 AG,DG 上的动点(与端点不重合),且∠DMN=∠DAM, 设 DN=x.
①求证四边形 AFGD 为菱形;
②是否存在这样的点 N,使△DMN 是直角三角形?若存在,请求出 x 的值;若不存在, 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
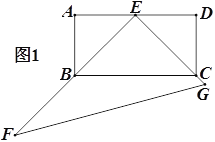
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
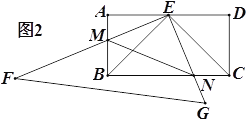
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
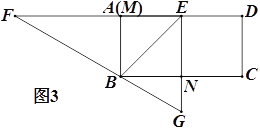
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,连接DC,点F、P、G分别为DE、DC、BC的中点.
(1)观察猜想:图1中,线段PF与PG的数量关系是 ,∠FPG= (用含α的代数式表示)
(2)探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出PF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com