
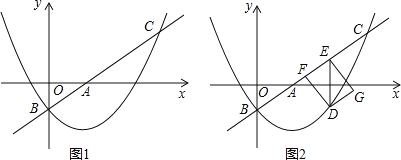
����Ŀ����ͼ 1���ھ��� ABCD �У�AB��8��AD��10��E �� CD ����һ�㣬���� AE�������� ABCD �� AE �۵������� D ǡ������ BC ���ϵ� F �����ӳ� AE �� BC ���ӳ����ڵ�G��
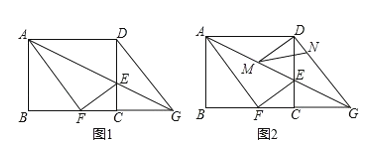
��1�����߶� CE �ij���
��2����ͼ 2��M��N �ֱ����߶� AG��DG �ϵĶ��㣨��˵㲻�غϣ����ҡ�DMN����DAM�� �� DN��x��
����֤�ı��� AFGD Ϊ���Σ�
���Ƿ���������ĵ� N��ʹ��DMN ��ֱ�������Σ������ڣ������ x ��ֵ���������ڣ� ��˵�����ɣ�
���𰸡���1��CE=3����2���ټ���������![]() ��2��
��2��
��������
��1���ɷ��ۿ�֪��AD��AF��10��DE��EF����EC��x����DE��EF��8x����Rt��ECF�У����ù��ɶ����������̼��ɽ�����⣮
��2�����ɡ�ADE�ס�GCE�����GC�ij��ȣ���֤���ı���AFGD��ƽ���ı��Σ�����һ���ڱ���ȵ�ƽ���ı��ε����μ���֤����
������DMN ��ֱ�������Σ��������������һ�ǵ���MDN=90��ʱ�����ǵ���DNM=90��ʱ���ֱ��������������ε������Լ�������Ǻ����Ķ��弴�ɼ���ó���
�⣺��1�����ı���ABCD�Ǿ��Σ�
��AD��BC��10��AB��CD��8��
���B����BCD��90����
�ɷ��ۿ�֪��AD��AF��10��DE��EF����CE��x����DE��EF��8x��
��Rt��ABF��BF��![]() ��
��
��CF��BCBF��106��4��
��Rt��EFC������(8x)2��x2��42��
��x��3��
��CE��3��
��2����֤�������ı���ABCD�Ǿ��Σ�
��AD��BC
���ADE�ס�GCE��
��![]() ��
��
��AD=10��CE=3��DE=5��
��![]() ��
��
��GC=6��
�ɣ�1���ɵã�CF=4��
��GF=6+4=10��
���ı���AFGD��ƽ���ı��Σ�
�֡�AD=AF��
��ƽ���ı���AFGD�����Σ�
�ڡߡ�DMN=��DAM��
������DMN ��ֱ�������Σ��������������
����MDN=90��ʱ��
��AD=GD��
���DAG=��DGA
�֡ߡ�ADE=��GDM=90����
���ADE�ա�GDM��ASA��
��DM=DE=5��
�֡ߡ�DMN=��DAM����ADE=��MDN=90����
���ADE�ס�MDN
��![]() ����
����![]() ��
��
��![]() ��
��
����DNM=90��ʱ�����MDN+��DMN=90����
�֡ߡ�DMN=��DAM����DAG=��DGA��
���DMN=��DGA��
���MDN+��DGA=90����
���DMG=90����
��sin��DAE=![]() ��
��
��![]() ��
��
��![]() ��
��
��DM=![]() ��
��
�ߡ�DMN=��DAM
��sin��DMN=sin��DAM
��![]() ����
����![]()
��ã�x=2��
����������![]() ��2��
��2��


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
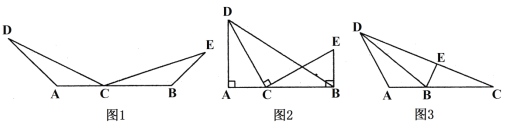
����Ŀ������ͼ1����C���߶�AB�ϣ���D��E��ֱ��ABͬ�࣬��A����DCE����CBE��DC��CE.��֤��AC��BE.
����ͼ2����C���߶�AB�ϣ���D��E��ֱ��ABͬ�࣬��A����DCE����CBE��90��.
����֤��![]() ��������BD������ADC����ABD��AC��3��BC��
��������BD������ADC����ABD��AC��3��BC��![]() ����tan��CDB��ֵ��
����tan��CDB��ֵ��
����ͼ3���ڡ�ABD�У���C��AB���ϣ��ҡ�ADC����ABD����E��BD���ϣ�����CE����BCE����BAD��180�㣬AC��3��BC��![]() ��CE��
��CE��![]() ��ֱ��д��
��ֱ��д��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
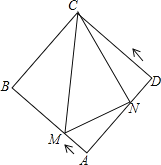
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4������M��Nͬʱ��A���������M��AB��ÿ��1����λ���ȵ��ٶ����е�B�˶�����N������ADC��ÿ��2����λ���ȵ��ٶ����յ�C�˶������˶�ʱ��Ϊt�룬����CMN�����ΪS����t������ͼ������ǣ�������
A. 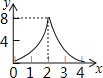 B.
B. 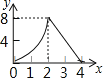
C. 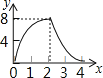 D.
D. 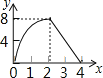
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ABCD���ĸ��ڽ�ƽ�����ཻ��E��F��G��H����֤���ı���EFGH�Ǿ��Ρ�
ABCD���ĸ��ڽ�ƽ�����ཻ��E��F��G��H����֤���ı���EFGH�Ǿ��Ρ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���ACB��90����AC��BC��DΪAB���е㣬��EΪAC�ӳ�����һ�㣬����DE������D��DF��DE��CB���ӳ����ڵ�F��
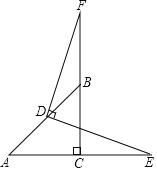
��1����֤��BF��CE��
��2����CE��AC���õ�ʽ��ʾ�߶�DF��AB��������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() ��ͼ���㣨��3��2����
��ͼ���㣨��3��2����
��1�������Ľ���ʽ��
��2����ֱ�������л����÷�����������ͼ��
��3������3��x����2����y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ų��л�����ķ�չ����ͨӵ�³�Ϊ�ϰ�߷�ʱ���Ա��������Ϊ�˽���Ȫ��ij����·��ͨӵ���������Ȫij��ѧͬѧ��ʵ��ͳ�Ʒ����о���������![]() ʱ�������ٶ�v��ǧ��/Сʱ���dz����ܶ�x����/ǧ�ף���һ�κ��������õ�·�ij����ܶȴﵽ220��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶ�Ϊ95��/ǧ��ʱ�������ٶ�Ϊ50ǧ��/Сʱ��
ʱ�������ٶ�v��ǧ��/Сʱ���dz����ܶ�x����/ǧ�ף���һ�κ��������õ�·�ij����ܶȴﵽ220��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶ�Ϊ95��/ǧ��ʱ�������ٶ�Ϊ50ǧ��/Сʱ��
��1����![]() ʱ�������ٶ�v��ǧ��/Сʱ���복���ܶ�x����/ǧ�ף��ĺ�����ϵʽ��
ʱ�������ٶ�v��ǧ��/Сʱ���복���ܶ�x����/ǧ�ף��ĺ�����ϵʽ��
��2��Ϊʹ�õ�·�ϳ����ٶȴ���40ǧ��/Сʱ��С��60ǧ��/Сʱ��Ӧ���Ƹõ�·�ϵij����ܶ���ʲô��Χ�ڣ�
��3������������/Сʱ���ǵ�λʱ����ͨ���õ�·��ij�۲��ij�����������������=�����ٶȡ������ܶȣ���![]() ʱ����õ�·�ϳ�����y�����ֵ����ʱ�����ٶ�Ϊ���٣�
ʱ����õ�·�ϳ�����y�����ֵ����ʱ�����ٶ�Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��x�ᡢy��ֱ��ڵ�A�͵�B��0��-1����������
��x�ᡢy��ֱ��ڵ�A�͵�B��0��-1����������![]() ������B������ֱ��l����һ������ΪC��4��n����
������B������ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ��ҵ�D�ĺ�����Ϊt��0<t<4����DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2����������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3��M��ƽ����һ�㣬����AOB�Ƶ�M����ʱ�뷽����ת90���õ���A'O'B'����A��O��B�Ķ�Ӧ��ֱ��ǵ�A'��O'��B'�� ����A'O'B'����������ǡ�������������ϣ���ֱ��д����A���ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ���ı���![]() ��,
��, ![]() ,����Ϊ
,����Ϊ![]() ��
��![]() ���ӳ����ཻ��
���ӳ����ཻ��![]() ,��
,��![]() ������
������![]() ��
��
(1)��ͼ![]() ,��֤:�ı���
,��֤:�ı���![]() �����Σ�
������
(2)��ͼ![]() ,����
,����![]() ,��
,��![]() ,�ڲ������κθ����ߵ������,ֱ��д��ͼ
,�ڲ������κθ����ߵ������,ֱ��д��ͼ![]() �������������
�������������![]() ������Ķ۽�������.
������Ķ۽�������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com