
����Ŀ�����ų��л�����ķ�չ����ͨӵ�³�Ϊ�ϰ�߷�ʱ���Ա��������Ϊ�˽���Ȫ��ij����·��ͨӵ���������Ȫij��ѧͬѧ��ʵ��ͳ�Ʒ����о���������![]() ʱ�������ٶ�v��ǧ��/Сʱ���dz����ܶ�x����/ǧ�ף���һ�κ��������õ�·�ij����ܶȴﵽ220��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶ�Ϊ95��/ǧ��ʱ�������ٶ�Ϊ50ǧ��/Сʱ��
ʱ�������ٶ�v��ǧ��/Сʱ���dz����ܶ�x����/ǧ�ף���һ�κ��������õ�·�ij����ܶȴﵽ220��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶ�Ϊ95��/ǧ��ʱ�������ٶ�Ϊ50ǧ��/Сʱ��
��1����![]() ʱ�������ٶ�v��ǧ��/Сʱ���복���ܶ�x����/ǧ�ף��ĺ�����ϵʽ��
ʱ�������ٶ�v��ǧ��/Сʱ���복���ܶ�x����/ǧ�ף��ĺ�����ϵʽ��
��2��Ϊʹ�õ�·�ϳ����ٶȴ���40ǧ��/Сʱ��С��60ǧ��/Сʱ��Ӧ���Ƹõ�·�ϵij����ܶ���ʲô��Χ�ڣ�
��3������������/Сʱ���ǵ�λʱ����ͨ���õ�·��ij�۲��ij�����������������=�����ٶȡ������ܶȣ���![]() ʱ����õ�·�ϳ�����y�����ֵ����ʱ�����ٶ�Ϊ���٣�
ʱ����õ�·�ϳ�����y�����ֵ����ʱ�����ٶ�Ϊ���٣�
���𰸡���1��v����![]() x+88����2��70��x��120����3��������y�����ֵ��ÿСʱ4840������ʱ�����ٶ���44ǧ��/ʱ��
x+88����2��70��x��120����3��������y�����ֵ��ÿСʱ4840������ʱ�����ٶ���44ǧ��/ʱ��
��������
��1����20��x��220ʱ���賵���ٶ�v�복���ܶ�x�ĺ�����ϵʽΪv��kx+b���ٸ��ݴ���ϵ������⼴�ɣ�
��2���ɣ�1���Ľ���ʽ��������ʽ�������⼯���ɣ�
��3���賵����y��x֮��Ĺ�ϵʽΪy��vx����20��x��220ʱ��ʾ����Ӧ�Ķ��κ�����ϵ���ɶ��κ��������ʾͿ�����������
�⣺��1���賵���ٶ�v�복���ܶ�x�ĺ�����ϵʽΪv��kx+b�������⣬��
![]() ����ã�
����ã�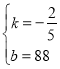 ��
��
�൱20��x��220ʱ��v����![]() x+88��
x+88��
��2�������⣬�ã�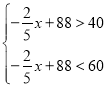 ����ã�70��x��120��
����ã�70��x��120��
��Ӧ���Ƹõ�·�ϵij����ܶ���70��x��120��Χ�ڣ�
��3���賵����y��x֮��Ĺ�ϵʽΪy��vx��
��20��x��220ʱ��y������![]() x+88��x����
x+88��x����![]() ��x��110��2+4840��
��x��110��2+4840��
�൱x��110ʱ��y���4840����ʱ![]() ǧ��/ʱ��
ǧ��/ʱ��
�൱�����ܶ���110��/ǧ��ʱ��������yȡ�����ֵ��ÿСʱ4840������ʱ�����ٶ���44ǧ��/ʱ��


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
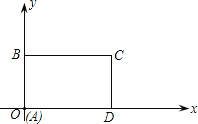
����Ŀ����ͼ��ʾ����ֱ������ϵ�У�����![]() �ı�
�ı�![]() ��
��![]() ���ϣ���
���ϣ���![]() ��ԭ�㣬
��ԭ�㣬![]() .��������ÿ��2����λ������
.��������ÿ��2����λ������![]() ���������������˶�.ͬʱ��
���������������˶�.ͬʱ��![]() �ӵ�
�ӵ�![]() ������ÿ��1����λ������
������ÿ��1����λ������![]() ��·���������˶�����
��·���������˶�����![]() ���˶���
���˶���![]() ��ʱֹͣ�˶�������
��ʱֹͣ�˶�������![]() Ҳ��ֹ֮ͣ�˶�.��
Ҳ��ֹ֮ͣ�˶�.��![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ���룩.
���룩.
��1����![]() ʱ�������
ʱ�������![]() �����ꣻ
�����ꣻ
��2����![]() �����Ϊ
�����Ϊ![]() �������
�������![]() ��
��![]() ֮��ĺ�����ϵʽ����д����Ӧ���Ա���
֮��ĺ�����ϵʽ����д����Ӧ���Ա���![]() ��ȡֵ��Χ��.
��ȡֵ��Χ��.
��3�������⣨2�����еĺ����Ĵ���ͼ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̾����ı�����·ݵ��ۼ۱�һ�·�ÿ̨����500Ԫ����֪������ͬ�����ı���һ�·ݵ����۶�Ϊ9��Ԫ�����·ݵ����۶�ֻ��8��Ԫ��
��1�����·ݱ���ÿ̨�ۼ�Ϊ����Ԫ��
��2��Ϊ��������þ����̼ƻ����·��ٹ���ϴ�»��������ۣ���֪ϴ�»�ÿ̨����Ϊ4000Ԫ������ÿ̨����Ϊ3500Ԫ��Ԥ���ò�����7.6��Ԫ���ʽ������ּҵ繲20̨�������Ϊy̨��y��12���������м��ֽ���������
��3�����·�Ϊ�˴������þ����̾����ڶ��·��ۼ۵Ļ����ϣ�ÿ�۳�һ̨�����ٷ����˿��ֽ�aԪ����ϴ�»���ÿ̨4400Ԫ���ۣ���������£�����2���и�������õ�������ͬ����aӦȡ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
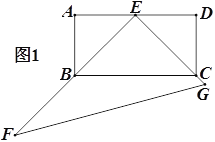
����Ŀ����ͼ 1���ھ��� ABCD �У�AB��8��AD��10��E �� CD ����һ�㣬���� AE�������� ABCD �� AE �۵������� D ǡ������ BC ���ϵ� F �����ӳ� AE �� BC ���ӳ����ڵ�G��
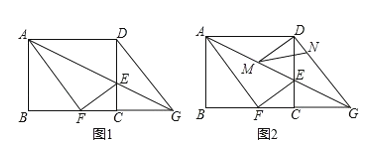
��1�����߶� CE �ij���
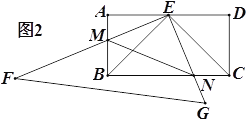
��2����ͼ 2��M��N �ֱ����߶� AG��DG �ϵĶ��㣨��˵㲻�غϣ����ҡ�DMN����DAM�� �� DN��x��
����֤�ı��� AFGD Ϊ���Σ�
���Ƿ���������ĵ� N��ʹ��DMN ��ֱ�������Σ������ڣ������ x ��ֵ���������ڣ� ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD�У�E��AD���е㣬�Ե�Eֱ�Ƕ����ֱ��������EFG������EF��EG�ֱ����B��C����F��30��.
��1����֤��BE��CE
��2������EFG�Ƶ�E��˳ʱ�뷽����ת������ת��EF��AD�غ�ʱֹͣת��.��EF��EG�ֱ���AB��BC�ཻ�ڵ�M��N.����ͼ2��
����֤����BEM�ա�CEN��
����AB��2�����BMN��������ֵ��
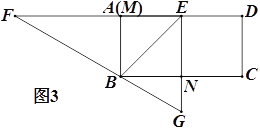
�۵���תֹͣʱ����Bǡ����FG�ϣ���ͼ3������sin��EBG��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2��
������![]() ����������x1=��1��x2=3��
����������x1=��1��x2=3��
��3a+c��0
����y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3
����x��0ʱ��y��x���������
���н�����ȷ�ĸ����ǣ�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������߾���A![]() ��B
��B![]() ��C
��C![]() ���㣮
���㣮
��1���������ߵĽ���ʽ��
��2������MΪ������������������һ���㣬��M�ĺ�����Ϊm����AMB�����ΪS����S����m�ĺ�����ϵʽ�������S�����ֵ��
��3������P���������ϵĶ��㣬��Q��ֱ��![]() �ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����㣬���Ķ����²��ϣ��������Ӧ�����⣮
��ƽ���߷��߶γɱ�����������ͼ1���ڡ�ABC�У�ADƽ�֡�BAC����![]() ��
��![]() ����������������IJ���֤�����̣�
����������������IJ���֤�����̣�
֤������ͼ2����C��CE��DA����BA���ӳ�����E����
����1���밴�������֤��˼·��д����֤����ʣ�ಿ�֣�
��2����գ���ͼ3����֪Rt��ABC�У�AB��3��BC��4����ABC��90�㣬ADƽ�֡�BAC�����ABD���ܳ����� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P��Q���������¶��壺��P��QΪij�������εĶ��㣬�ұ�PQ�ϵĸ�h������h��PQ����Ƹ�������Ϊ��P��Q������������������
��1����֪��A��4��0����
�������߶�OAΪ��ij����������ǡ���ǵ�O��A��������������������������ε�������
����Rt��ABC�ǵ�A��B�������������������ҵ�B��x���ϣ���C��ֱ��y��2x��5�ϣ����B������Ϊ�� ����
��2����T��Բ��Ϊ��T��2��0�����뾶Ϊ2����M������Ϊ��2��6����NΪֱ��y��x+4��һ�㣬������Rt��MND���ǵ�M��N�������������������ұ�ND���T�й����㣬ֱ��д����N�ĺ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com