
【题目】阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则![]() =
=![]() .下面是这个定理的部分证明过程.
.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .

【答案】(1)见解析;(2)![]()
【解析】
(1)过C作CE∥DA.交BA的延长线于E,利用平行线分线段成比例定理得到![]() =
=![]() ,利用平行线的性质得∠2=∠ACE,∠1=∠E,由∠1=∠2得∠ACE=∠E,所以AE=AC,于是有
,利用平行线的性质得∠2=∠ACE,∠1=∠E,由∠1=∠2得∠ACE=∠E,所以AE=AC,于是有![]() =
=![]() ;
;
(2)先利用勾股定理计算出AC=5,再利用(1)中的结论得到![]() =
=![]() ,即
,即![]() =
=![]() ,则可计算出BD=
,则可计算出BD=![]() ,然后利用勾股定理计算出AD=
,然后利用勾股定理计算出AD=![]() ,从而可得到△ABD的周长.
,从而可得到△ABD的周长.
(1)过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴![]() =
=![]() ,∠2=∠ACE,∠1=∠E,
,∠2=∠ACE,∠1=∠E,
∵AD平分∠BAC
∴∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴![]() =
=![]() ;
;
(2)∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BD=![]() ,
,
∴AD=![]() =
=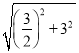 =
=![]() ,
,
∴△ABD的周长=![]() +3+
+3+![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
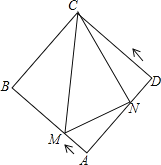
【题目】如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
A. 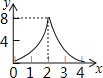 B.
B. 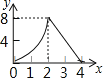
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城市化建设的发展,交通拥堵成为上班高峰时难以避免的现象.为了解龙泉驿某条道路交通拥堵情况,龙泉某中学同学经实地统计分析研究表明:当![]() 时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
(1)当![]() 时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
(2)为使该道路上车流速度大于40千米/小时且小于60千米/小时,应控制该道路上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过该道路上某观测点的车辆数,即:车流量=车流速度×车流密度.当![]() 时,求该道路上车流量y的最大值.此时车流速度为多少?
时,求该道路上车流量y的最大值.此时车流速度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
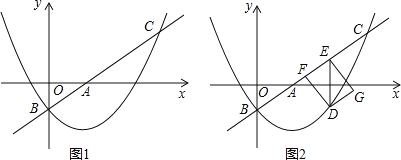
【题目】如图1,在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴、y轴分别交于点A和点B(0,-1),抛物线
与x轴、y轴分别交于点A和点B(0,-1),抛物线![]() 经过点B,且与直线l的另一个交点为C(4,n).
经过点B,且与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,且点D的横坐标为t(0<t<4),DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A'O'B',点A、O、B的对应点分别是点A'、O'、B'. 若△A'O'B'的两个顶点恰好落在抛物线上,请直接写出点A’的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
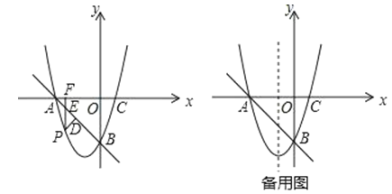
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A,C(1,0),与y轴交于点B(0,﹣3).
(1)求抛物线的解析式;
(2)点P是直线AB下方的抛物线上一动点,过点P作x轴的垂线,垂足为点F,交直线AB于点E,作PD⊥AB于点D.当△PDE的周长最大时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]()
![]() 经过点
经过点![]() .
.
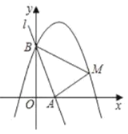
(1)求该抛物线的函数表达式:
(2)已知点![]() 是抛物线上的一个动点,并且点
是抛物线上的一个动点,并且点![]() 在第一象限内,连接
在第一象限内,连接![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数表达式,并求出
的函数表达式,并求出![]() 的最大值;
的最大值;
(3)在(2)的条件下,当![]() 取得最大值时动点
取得最大值时动点![]() 相应的位置记为点
相应的位置记为点![]() ,写出点
,写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
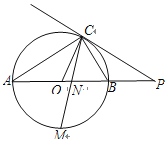
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为 ;
(2)如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;
(3)如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y=![]() (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为
(x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为![]() .当△ABC是直角三角形时,求 k 的值.
.当△ABC是直角三角形时,求 k 的值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com