
【题目】如图,ABCD中,AB=2cm,AC=5cm,SABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.
(1)在运动过程中,四边形AECF的形状是____;
(2)t=____时,四边形AECF是矩形;
(3)求当t等于多少时,四边形AECF是菱形.

【答案】(1)四边形AECF是平行四边形;理由见解析;(2)t=1;(3)t=![]()
【解析】
(1)由平行四边形的性质得出AB=CD=2cm,AB∥CD,由已知条件得出CF=AE,即可得出四边形AECF是平行四边形;
(2)若四边形AECF是矩形,则∠AFC=90°,得出AF⊥CD,由平行四边形的面积得出AF=4cm,在Rt△ACF中,由勾股定理得出方程,解方程即可;
(3)当AE=CE时,四边形AECF是菱形.过C作CG⊥BE于G,则CG=4cm,由勾股定理求出AG,得出GE,由勾股定理得出方程,解方程即可.
解:(1)四边形AECF是平行四边形;理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD=2cm,AB∥CD,
∴CF∥AE,
∵DF=BE,
∴CF=AE,
∴四边形AECF是平行四边形;
故答案为:平行四边形;
(2)t=1时,四边形AECF是矩形;理由如下:
若四边形AECF是矩形,
∴∠AFC=90°,
∴AF⊥CD,
∵SABCD=CDAF=8cm2,
∴AF=4cm,
在Rt△ACF中,AF2+CF2=AC2,
即42+(t+2)2=52,
解得:t=1,或t=-5(舍去),
∴t=1;故答案为:1;
(3)依题意得:AE平行且等于CF,
∴四边形AECF是平行四边形,
故AE=CE时,四边形AECF是菱形.
又∵BE=tcm,
∴AE=CE=t+2(cm),
过C作CG⊥BE于G,如图所示:
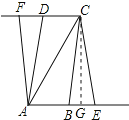
则CG=4cm
AG=![]() =3(cm),
=3(cm),
∴GE=t+2-3=t-1(cm),
在△CGE中,由勾股定理得:CG2+GE2=CE2=AE2,
即42+(t-1)2=(t+2)2,
解得:t=![]() ,
,
即t=![]() s时,四边形AECF是菱形.
s时,四边形AECF是菱形.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】操作:将一把三角尺放在如图①的正方形![]() 中,使它的直角顶点
中,使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() ,探究:
,探究:
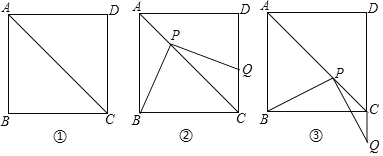
(1)如图②,当点![]() 在
在![]() 上时,求证:
上时,求证:![]() .
.
(2)如图③,当点![]() 在
在![]() 延长线上时,①中的结论还成立吗?简要说明理由.
延长线上时,①中的结论还成立吗?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
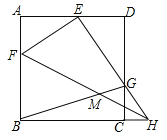
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( )

A. 669 B. 670 C. 671 D. 672
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探究
宽与长的比是![]() (约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
(约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
下面我们通过折纸得到黄金矩形。
第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。

第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是![]() 。
。
第三步,折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处,折痕为
处,折痕为![]() 。
。
第四步,展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ;过点
;过点![]() 折出折痕
折出折痕![]() ,使
,使![]() 。
。

(1)上述第三步将![]() 折到
折到![]() 处后,得到一个四边形
处后,得到一个四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由。
的形状,并说明理由。
(2)上述第四步折出折痕![]() 后得到一个四边形
后得到一个四边形![]() ,这个四边形是黄金矩形,请你说明理由。(提示:设
,这个四边形是黄金矩形,请你说明理由。(提示:设![]() 的长度为2)
的长度为2)
(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形![]() 除外,直接写出答案,不需证明,可能参考数值:
除外,直接写出答案,不需证明,可能参考数值:![]() )
)
(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借助下面的材料,
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如|5﹣3|表示5、3在数轴上对应的两点之间的距离:|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离:|5|=|5﹣0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A点B在数轴上分别表示有理数a,b,那么点A、点B之间的距离可表示为|a﹣b|.
问题:如图,数轴上A,B两点对应的有理数分别为﹣8和12,点P从点O出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)求经过2秒后,数轴点P、Q分别表示的数;
(2)当t=3时,求PQ的值;
(3)在运动过程中是否存在时间t使AP=![]() AB,若存在,请求出此时t的值,若不存在,请说明理由.
AB,若存在,请求出此时t的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com