
����������10�֣�
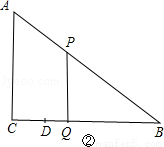
��ͼ1����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm����D��BC��һ����.����P��C��������2cm/s���ٶ���C��A��B�����˶�������Q��D��������1cm/s���ٶ���D��B�����˶�.��P����5 s��Q�ſ�ʼ�������ҵ�һ����ﵽBʱ����һ������ֹ֮ͣ��ͼ2�ǵ� ʱ��BPQ�����S�� cm2�����P���˶�ʱ��t��s���ĺ���ͼ��.
ʱ��BPQ�����S�� cm2�����P���˶�ʱ��t��s���ĺ���ͼ��.

��1��CD = ��  ��
��
��2������P�ڱ�AB��ʱ��tΪ��ֵʱ��ʹ�á�BPQ���ABCΪ���ƣ�
��3���˶������У��������BPQ����BPΪ���ĵ���������ʱt��ֵ.
��1��CD=2��a=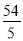 ����2��4.25���6�룻��3��5���
����2��4.25���6�룻��3��5���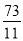 �룮
�룮
��������
�����������1�����ݺ���ͼ��õ�����P�˶�����Aʱ����BPQ�����Ϊ18�����������������ʽ�ɼ����BD=6����CD=2����t=5sʱ��AP=4����Q��D�㣬��PH��BC��H����Rt��ABC�и��ݹ��ɶ��������AB=10����֤����BPH�ס�BAC���������Ʊȼ����PH��Ȼ����������������ʽ�õ�S��PBQ����a=S��PBQ��
��2���������ۣ���3��t��5����Q��D�㣬BP=16��2t����PD��BC�õ���BPQ�ס�BAC���������Ʊȵ�tֵ����5��t��8��DQ=t��5��BQ=11��t��BP=16��2t������PQB=90��ʱ����BPQ�ס�BAC���������Ʊȵ�tֵ������BPQ=90��ʱ����BPQ�ס�BAC���������Ʊȵ�tֵ��
��3��PB=16��2t��BQ=11��t���������ۣ���BP=BQ����16��2t=11��t���ⷽ�̵�t=5����PB=PQ����PM��BC��M�����ݵ��������ε����ʵ���BM=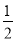 BQ=
BQ=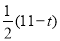 ����֤����BPM�ס�BAC���������Ʊȵ�tֵ��
����֤����BPM�ס�BAC���������Ʊȵ�tֵ��
�����������1������P�˶�����Aʱ����BPQ�����Ϊ18����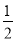 •6BD=18�����BD=6��
•6BD=18�����BD=6��
��CD=BC��BD=2��
��t=5sʱ��AP=2��5��6=4����Q��D�㣬��P��AB����ͼ�٣���PH��BC��H��
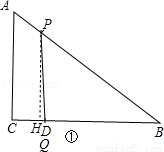
��Rt��ABC��AC=6��BC=8����AB=10��
��PH��AC�����BPH�ס�BAC����PH��AC=BP��BA����PH��6=(10��4)��10�����PH=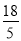 ��
��
��S��PBQ=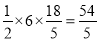 ����
����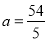 ���ʴ�Ϊ��2��
���ʴ�Ϊ��2��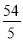 ��
��
��2����P�ڱ�AB�ϣ�
��3��t��5����Q��D�㣬BP=16��2t��
��PD��BC����BPQ�ס�BAC����BP��BA=BD��BC����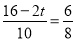 �����
�����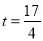 ��
��
��5��t��8��DQ=t��5����BQ=8��2����t��5��=11��t��BP=16��2t��
����PQB=90��ʱ����BPQ�ס�BAC����ͼ�ڣ�
�ߡ�BPQ�ס�BAC����BP��BA=BQ��BC����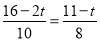 �����
�����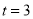 ������������ȥ��
������������ȥ��
����BPQ=90��ʱ����BPQ�ס�BAC����ͼ�ۣ�

�ߡ�BPQ�ס�BCA����BP��BC=BQ��BA����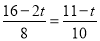 �����
�����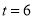 ��
��
������������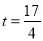 ��
��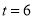 ʱ����BPQ���ABCΪ���ƣ�
ʱ����BPQ���ABCΪ���ƣ�
��3��PB=16��2t��BQ=11��t��
��BP=BQ����16��2t=11��t�����t=5��
��PB=PQ����PM��BC��M����ͼ�ܣ���BM=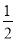 BQ=
BQ=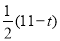 ��
��
��PM��AC�����BPM�ס�BAC����BP��BA=BM��BC���� �����
�����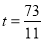 ��
��
��������������BPQ����BPΪ���ĵ���������ʱt��ֵΪ5��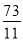 ��
��

���㣺1���������ۺ��⣻2����������ĺ���ͼ��3�����ɶ�����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����г簲�����꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
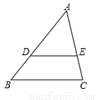
��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC�ϣ�DE��BC����AD��4��DB��2����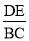 ��ֵΪ .
��ֵΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������12�֣���ͼ����֪l1��l2����O��l1��l2�����У���O�İ뾶Ϊ1cm������ABCD�ı�AD��AB�ֱ���l1��l2�غϣ�AB=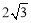 cm��AD=2cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ2cm/s������ABCD���ƶ��ٶ�Ϊ3cm/s�����ƶ�ʱ��Ϊt��s��.
cm��AD=2cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ2cm/s������ABCD���ƶ��ٶ�Ϊ3cm/s�����ƶ�ʱ��Ϊt��s��.

��1����ͼ�٣�����OA��AC�����OAC�Ķ���Ϊ �㣻
��2����ͼ�ڣ�����ͼ���ƶ�һ��ʱ���O�����O1��λ�ã�����ABCD����A1B1C1D1��λ�ã���ʱ��O1��A1��C1ǡ����ͬһֱ���ϣ���Բ��O�ƶ��ľ��루��OO1�ij�����
��3�����ƶ������У�Բ��O�����ζԽ���AC����ֱ�ߵľ����ڲ��ϱ仯����þ���Ϊd��cm������d��1ʱ����t��ȡֵ��Χ�����ʱ�������ñ���ͼ�������ʾ��ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��һԪ���η��� ����һ����ʽΪ .
����һ����ʽΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
����˵���У�����ȷ���ǣ� ��
A����Բ�ĵ�����Բ��ֱ��
B���Ȼ��ij���һ�����
C���ܳ���ȵ�����Բ�ǵ�Բ
D����ȵ������Ե�Բ�ܽ�Ҳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������8�֣���ͼ����ƽ��ֱ������ϵ�У���AOB�Ķ�������ֱ�ΪA��2��1����O��0��0����B��1����2��.

��1��P��a��b���ǡ�AOB�ı�AB��һ�㣬��AOB��ƽ�ƺ��P�Ķ�Ӧ��ΪP2��a��3�� b+1�����뻭������ƽ�ƺ�ġ�A1O1B1����д����A1�����ꣻ
��2���Ե�OΪλ�����ģ���y����Ҳ����AOB��һ��λ�ơ�A2OB2��ʹ�����AOB�����Ʊ�Ϊ2��1�����ֱ�д����A��P�Ķ�Ӧ��A2��P2�����ꣻ
��3���жϡ�A2OB2���A1O1B1�ܷ��ǹ���ijһ��QΪλ�����ĵ�λ��ͼ�Σ����ǣ�����ͼ10�б��λ������Q����д����Q������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ�������ǰ��ֱ�Ƕ�����ڡ�O��Բ���ϣ�����ֱ�DZ߷ֱ�O��A��B���㣬��P���Ż�AB�ϣ������A��B���غϣ�����PA��PB.���APB�Ĵ�СΪ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
������8�֣���ͼ1�����ı���ABCD�У�DC��AB��AD=BC, BDƽ�֡�ABC��

��1����֤��AD=DC��
��2����ͼ2�������������£�����A=��ABC= 60O������D��DE��AB������C��CF��BD������ֱ�ΪE��F������EF���жϡ�DEF����״��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ƽ��ֱ������ϵ�У��Ե㣨3����5��ΪԲ�ģ�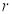 Ϊ�뾶��Բ�����ҽ������㵽
Ϊ�뾶��Բ�����ҽ������㵽 ������ֱ�ߵľ������1����Բ�İ뾶
������ֱ�ߵľ������1����Բ�İ뾶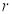 ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com