
����������12�֣���ͼ����֪l1��l2����O��l1��l2�����У���O�İ뾶Ϊ1cm������ABCD�ı�AD��AB�ֱ���l1��l2�غϣ�AB=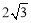 cm��AD=2cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ2cm/s������ABCD���ƶ��ٶ�Ϊ3cm/s�����ƶ�ʱ��Ϊt��s��.
cm��AD=2cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ2cm/s������ABCD���ƶ��ٶ�Ϊ3cm/s�����ƶ�ʱ��Ϊt��s��.

��1����ͼ�٣�����OA��AC�����OAC�Ķ���Ϊ �㣻
��2����ͼ�ڣ�����ͼ���ƶ�һ��ʱ���O�����O1��λ�ã�����ABCD����A1B1C1D1��λ�ã���ʱ��O1��A1��C1ǡ����ͬһֱ���ϣ���Բ��O�ƶ��ľ��루��OO1�ij�����
��3�����ƶ������У�Բ��O�����ζԽ���AC����ֱ�ߵľ����ڲ��ϱ仯����þ���Ϊd��cm������d��1ʱ����t��ȡֵ��Χ�����ʱ�������ñ���ͼ�������ʾ��ͼ����
��1��105�㣻��2�� ����3��
����3�� ��
��
��������
�����������1���������ߵ������Լ�������Ǻ�����ϵ�ֱ������OAD=45�㣬��DAC=60�㣬�����ó��𰸣�
��2�����ȵó�����C1A1D1=60�㣬������A1E=AA1��OO1��1=t��1�����t��ֵ�������ó�OO1=2t�ó��𰸼��ɣ�
��3���ٵ�ֱ��AC���O��һ������ʱ�����ƶ�ʱ��Ϊt1���ڵ�ֱ��AC���O�ڶ�������ʱ�����ƶ�ʱ��Ϊt2���ֱ�������ɣ�
�����������1����l1��l2����O��l1��l2�����У����OAD=45�㣬
��AB=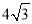 cm��AD=4cm����CD=
cm��AD=4cm����CD=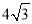 cm��AD=4cm����tan��DAC=
cm��AD=4cm����tan��DAC=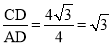 �����DAC=60�㣬���OAC�Ķ���Ϊ����OAD+��DAC=105�㣬
�����DAC=60�㣬���OAC�Ķ���Ϊ����OAD+��DAC=105�㣬
�ʴ�Ϊ��105��
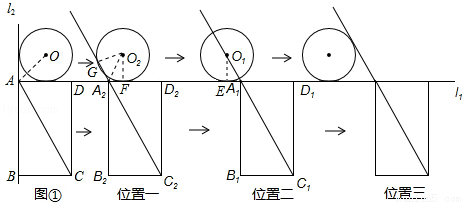
��2����ͼλ�ö�����O1��A1��C1ǡ����ͬһֱ����ʱ�����O1��l1���е�ΪE��
����O1E���ɵ�O1E=2��O1E��l1��
��Rt��A1D1C1����A1D1=4��C1D1= ����tan��C1A1D1=
����tan��C1A1D1= �����C1A1D1=60�㣬
�����C1A1D1=60�㣬
��Rt��A1O1E�У���O1A1E=��C1A1D1=60�㣬��A1E= ��
��
��A1E=AA1��OO1��1=t��1����t��1=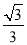 ����t=
����t= ����OO1=2t=
����OO1=2t=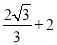 ��
��
��3���ٵ�ֱ��AC���O��һ������ʱ�����ƶ�ʱ��Ϊt1��
�� �� ��t1=1��
�� ��t1=1�� ��
��
�ڵ�ֱ��AC���O�ڶ�������ʱ�����ƶ�ʱ��Ϊt2�� ����ã�
����ã� ��
��
��d��1ʱ���Խ���AC����ֱ�����O�ཻ����t��ȡֵ��Χ�ǣ� ��
��
���㣺Բ���ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����л�ɽ�����꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��д��һ�����̵Ľ���2��һԪһ�η��̣� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����г簲�����꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
ԭ��168Ԫ����Ʒ�������ν���a%���ۼ�Ϊ128Ԫ�����з�����ȷ���ǣ� ��
A��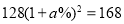
B��
C��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
�����������ε�һ����Ϊ80�㣬��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
����˵����ȷ���ǣ� ��
A��������4.60��ȷ��ʮ��λ
B��������5000��ȷ����λ
C��������4.31��ȷ��0.01
D��1.45 104��ȷ����λ
104��ȷ����λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������8�֣����� ��һԪ���η���
��һԪ���η��� ������ʵ�������ֱ�Ϊ
������ʵ�������ֱ�Ϊ ��
��
��1���� ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���� ����
���� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪A��B��C���㶼�ڡ�O�ϣ���AOB=50�㣬��ACB= _________ �㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������10�֣�
��ͼ1����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm����D��BC��һ����.����P��C��������2cm/s���ٶ���C��A��B�����˶�������Q��D��������1cm/s���ٶ���D��B�����˶�.��P����5 s��Q�ſ�ʼ�������ҵ�һ����ﵽBʱ����һ������ֹ֮ͣ��ͼ2�ǵ� ʱ��BPQ�����S�� cm2�����P���˶�ʱ��t��s���ĺ���ͼ��.
ʱ��BPQ�����S�� cm2�����P���˶�ʱ��t��s���ĺ���ͼ��.

��1��CD = ��  ��
��
��2������P�ڱ�AB��ʱ��tΪ��ֵʱ��ʹ�á�BPQ���ABCΪ���ƣ�
��3���˶������У��������BPQ����BPΪ���ĵ���������ʱt��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
���������뷨�õ��Ľ����� 8.8��103 ��ȷ�� λ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com