
����Ŀ��ijˮ���̵���12.5Ԫ/ǧ�˵ļ۸�һ��ˮ���������ۣ�����������������5%�����������0.8Ԫ/ǧ�ˣ�������ð��ս����������㣩�����費���������ã�
��1���̵�Ҫ��ˮ��������������Ϊ����Ԫ�Ų��������
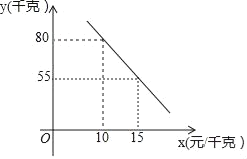
��2�������۹����У��̵귢��ÿ��ˮ����������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵ��ͼ��ʾ����ô�����۵��۶�Ϊ����ʱ��ÿ���õ�����w�����������Ƕ��٣�
��3�����̵����ÿ����1ǧ��ˮ���;���pԪ����p��1����ϣ�����̣�ͨ�����ۼ�¼���֣����ۼ۸����ÿǧ��22Ԫʱ���۳�������ÿ���������x�������С��ֱ��д��p��ȡֵ��Χ��
���𰸡���1��ˮ����Ҫ��ˮ���ۼ����ٶ�Ϊ14Ԫ/ǧ�˲Ų��������2�������۵��۶�Ϊ20Ԫʱ��ÿ���õ�����w������������180Ԫ��3��1��p��4
��������
��1���蹺��ˮ��aǧ�ˣ�ˮ���ۼ۶�ΪmԪ/ǧ�ˣ�ˮ���̲Ų�����������������г�����ʽ������⣻
��2���ɣ�1����y�����۵���x֮��ĺ�����ϵΪ��y����5x+130������w����x��14��y�õ����κ������ɽ�����⣻
��3����۳�����������Ϊs����s����x��14��p������5x+130�������ݶԳ����뺯�������ʼ������.
��1���蹺��ˮ��aǧ�ˣ�ˮ���ۼ۶�ΪmԪ/ǧ�ˣ�ˮ���̲Ų������������
am��1��5%���ݣ�12.5+0.8��a
��a��0�ɽ�ã�m��14
��ˮ����Ҫ��ˮ���ۼ����ٶ�Ϊ14Ԫ/ǧ�˲Ų������
��2���ɣ�1����֪��ÿǧ��ˮ����ƽ���ɱ�Ϊ14Ԫ
��y�����۵���x֮��ĺ�����ϵΪ��y����5x+130
������ã�w����x��14��y����x��14������5x+130������5x2+200x��1820
������w����5��x��20��2+180
�൱x��20ʱ��w�����ֵ
�൱���۵��۶�Ϊ20Ԫʱ��ÿ���õ�����w������������180Ԫ��
��3����۳�����������Ϊs
��s����x��14��p������5x+130������5x2+��5p+200��x��130��p+14��
�������ߵĿ�������
��Գ���Ϊֱ��x��![]() ��
��![]()
�����ۼ۸����ÿǧ��22Ԫʱ���۳�������ÿ�������s��x���������С
��![]() ��22
��22
���p��4
��1��p��4


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ա�ABD����E�ڱ�AB�ϣ�CE��BD������DE��
��֤����1����CEB=��CBE��
��2���ı���BCED�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
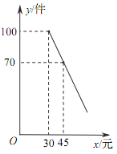
����Ŀ��ij�̵깺��һ���ɱ�Ϊÿ�� 30 Ԫ����Ʒ�������鷢�֣�����Ʒÿ��������� y�����������۵��� x��Ԫ��֮������һ�κ�����ϵ����ͼ����ͼ��ʾ.
��1�������Ʒÿ��������� y �����۵��� x ֮��ĺ�����ϵʽ��
��2�����̵갴���۲����ڳɱ��ۣ��Ҳ����� 50 Ԫ���ۣ������۵��۶�Ϊ���٣�����ʹ���۸���Ʒÿ���õ����� w��Ԫ�������������Ƕ��٣�
��3�����̵�Ҫʹ���۸���Ʒÿ���õ������� 800 Ԫ����ÿ�������������ӦΪ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У�E��F�ǶԽ���BD�ϲ�ͬ�����㣬���������У����ܵó��ı���AECFһ��Ϊƽ���ı��ε��ǣ� ��
A. BE=DF B. AE=CF C. AF//CE D. ��BAE=��DCF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������ABC�߳��Ƕ�ֵ����O���������ģ�����O������һ��ֱ�߷ֱ�AB��BC�ڵ�D��E������BDE��ֱ��DE�۵����õ���B��DE����B��D��B��E�ֱ�AC�ڵ�F��G������OF��OG���������жϴ�����ǣ�������
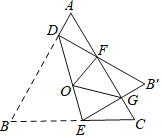
A. ��ADF�ա�CGE
B. ��B��FG���ܳ���һ����ֵ
C. �ı���FOEC�������һ����ֵ
D. �ı���OGB'F�������һ����ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
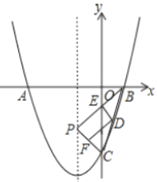
����Ŀ����ͼ������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �������߶Գ���������һ�㣬����
�������߶Գ���������һ�㣬����![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ����
����![]() ����СֵΪ_____��
����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
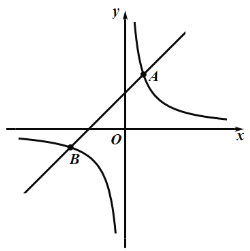
����Ŀ����ͼ������������ ��һ�κ��� ��ͼ����A(1��3)��B(-3��n)���㣮
��1������������һ�κ����Ľ���ʽ��
��2����xȡʲôֵʱ��һ�κ�����ֵ���ڷ�����������ֵ��
��3�������OAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
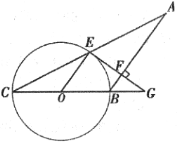
����Ŀ����ͼ������ABC�У�AB=BC����BCΪֱ������ O��AC�ڵ�E������E��AB�Ĵ��߽�AB�ڵ�F����CB���ӳ����ڵ�G��
��1����֤��EG�ǡ�O�����ߣ�
��2����BG=OB��AC=6����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��m��6����B��3��n������.
��ͼ����A��m��6����B��3��n������.
��1����һ�κ����Ľ���ʽ��
��2����![]() �������
�������
��3������ͼ��ֱ��д��![]() ��x��ȡֵ��Χ
��x��ȡֵ��Χ

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com