
【题目】已知:如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B.
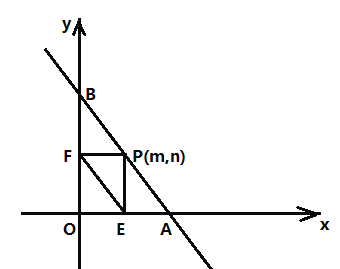
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,若△PEF的面积为S,求S关于m的函数关系式,并写出m的取值范围;
(3)以上(2)中的函数图象是一条直线吗?请尝试作图验证.
【答案】(1)A(4,0);(2)S△PET=-m2+4m,(0<m<4);(3)见解析
【解析】
(1)根据坐标轴上点的特点直接求值,
(2)由点在直线AB上,找出m与n的关系,再用三角形的面积公式求解即可;
(3)列表,描点、连线即可.
(1)解:令x=0,则y=8,
∴B(0、8)
令y=0,则2x+8=0
x=4
A(4,0),
(2)解:点P(m,n)为线段AB上的一个动点,
-2m+8=n,
∵A(4.0)
OA=4
∴0<m<4
∴S△PEF= ![]() PF×PE=
PF×PE= ![]() ×m×(-2m+8)=2(-2m+8)=-m2+4m,(0<m<4);
×m×(-2m+8)=2(-2m+8)=-m2+4m,(0<m<4);
(3)S关于m的函数图象不是一条直线,简图如下:
①列表
x | 0 | 0.5 | 1 | 1.5 | 12 | 2.5 | 3 | 3.5 | 4 |
y | 0 | 0.75 | 3 | 3.75 | 4 | 3.75 | 3 | 0.75 | 0 |
②描点,连线(如图)



 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
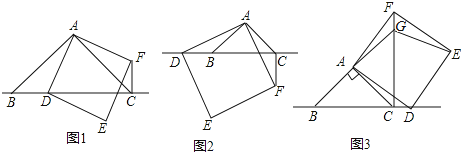
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系,
②BC,CD,CF之间的数量关系为;
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;
若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,求CF,EG.
BC,求CF,EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

查看答案和解析>>
科目:初中数学 来源: 题型:
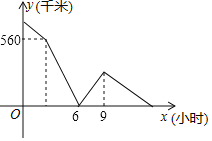
【题目】A、B、C三地在同一直线上,甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时).y与x的关系如图所示,则B、C两地相距_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
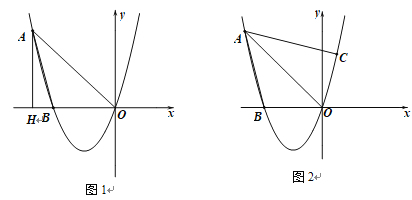
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx与x轴相交于点B(-3,0).
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,,试探究:在抛物线上是否存在点C,使∠CAO=∠BAO?若存在,请求出直线AC解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四座城市A,B,C,D分别位于一个边长100km的大正方形的四个顶点,由于各城市之间的商业往来日益频繁,于是政府决定修建公路网连接它们,根据实际,公路总长设计得越短越好,公开招标的信息发布后,一个又一个方案被提交上来,经过初审后,拟从下面四个方案中选定一个再进一步认证,其中符合要求的方案是( )

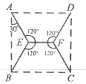
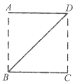
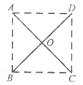
A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com