
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx与x轴相交于点B(-3,0).
(1)求抛物线的解析式;
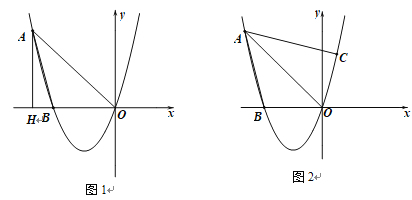
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,,试探究:在抛物线上是否存在点C,使∠CAO=∠BAO?若存在,请求出直线AC解析式;若不存在,请说明理由.
【答案】(1)y=x2+3x;(2)90°;(3)![]() .
.
【解析】
(1)将点A、B、C的坐标代入抛物线的解析式求解即可;
(2)由已知A(-4,4)则可得到OA的解析式,设点P的坐标为(m,m2+3m),则点Q的坐标为(m,-m).由题意可知QP=4,则-m-(m2+3m)=4,则可求得a的值,于是得到P(-2,-2),Q(-2,2),最后利用勾股定理的逆定理证明△OPQ为直角三角形即可;
(3)设AC交y轴于点D,根据题意证明△ABO≌△AOD,则OD=OB=3,设AC的解析式为y=px+q,将点A和点D的坐标代入求解即可.
(1)抛物线的解析式为![]()
(2)设点P坐标为![]() ,其中
,其中![]()
∵点A(-4,4),∴直线OA的解析式为![]() ,
,
从而点Q的坐标为![]() ,∴
,∴![]() =
=![]()
当四边形AHPQ为平行四边形时,PQ=AH=4,
即![]() ,解得
,解得![]() ,此时点P坐标为
,此时点P坐标为![]()
∴∠AOP=∠AOH+∠POH=45o+45o=90o.
(3)设AC交y轴于点D,由点A(-4,4)得,![]() ,
,
∵∠CAO=∠BAO,![]() ,∴
,∴![]() ≌
≌![]()
∴![]() ,点D坐标为(0,3)
,点D坐标为(0,3)
设直线AC解析式为![]() ,则
,则![]()
解得![]() ,
,![]() ,∴直线AC解析式为
,∴直线AC解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽发展了“重差术”,用于测量不可到达的物体的高度,比如,通过下列步骤可测量山的高度PQ(如图):
(1)测量者在水平线上的A处竖立一根竹竿,沿射线QA方向走到M处,测得山顶P、竹竿顶端B及M在一条直线上;
(2)将该竹竿竖立在射线QA上的C处,沿原方向继续走到N处,测得山顶P、竹竿顶端D及N在一条直线上;
(3)设竹竿与AM、CN的长分别为![]() 、a1、a2,可得公式:PQ=
、a1、a2,可得公式:PQ=![]() +
+![]() .则上述公式中,d表示的是( )
.则上述公式中,d表示的是( )
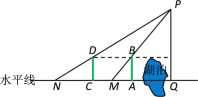
A. QA的长 B. AC的长 C. MN的长 D. QC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B.
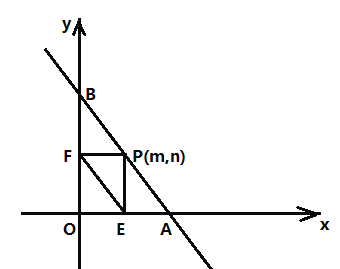
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,若△PEF的面积为S,求S关于m的函数关系式,并写出m的取值范围;
(3)以上(2)中的函数图象是一条直线吗?请尝试作图验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F,
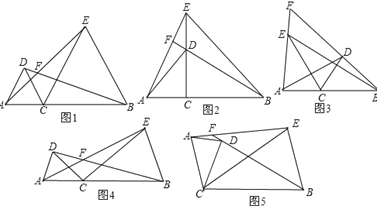
(1)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;如图3,若∠ACD=120°,则∠AFB= ;
(2)如图4,若∠ACD=α,则∠AFB= (用含α的式子表示);
(3)将图4中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),变成如图5所示的情形,若∠ACD=α,则∠AFB与α的有何数量关系?并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
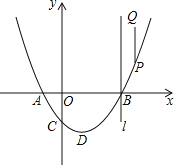
【题目】如图,已知抛物线![]() :
:![]() ,
,![]() 交x轴于A,
交x轴于A,![]() 点A在点B左边
点A在点B左边![]() ,交y轴于C,其顶点为D,P是
,交y轴于C,其顶点为D,P是![]() 上一个动点,过P沿y轴正方向作线段
上一个动点,过P沿y轴正方向作线段![]() 轴,使
轴,使![]() ,当P点在
,当P点在![]() 上运动时,Q随之运动形成的图形记为
上运动时,Q随之运动形成的图形记为![]() .
.
![]() 若
若![]() ,求点P运动到D点时点Q的坐标,并直接写出图形
,求点P运动到D点时点Q的坐标,并直接写出图形![]() 的函数解析式;
的函数解析式;
![]() 过B作直线
过B作直线![]() 轴,若直线l和y轴及
轴,若直线l和y轴及![]() ,
,![]() 所围成的图形面积为12,求t的值.
所围成的图形面积为12,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午![]() ,下午
,下午![]() ,每月
,每月![]() 天;
天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于![]() 件.
件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品数(件) | 生产乙产品数(件) | 所用时间 (分) |
|
|
|
|
|
|
信息三:按件计酬:每生产一件甲产品可得![]() 元,每生产一件乙产品可得
元,每生产一件乙产品可得![]() 元.
元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;
(2)小王该月最多能得多少元,此时生产甲、乙两种产品分别多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
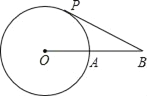
【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com