
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F。

(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③,你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由。
【答案】(1)证明见解析;(2)成立,证明见解析;(3)成立,证明见解析.
【解析】
试题分析:(1)利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF,进而得出答案;
(2)利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF,进而得出答案;
(3)利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF,进而得出答案.
试题解析:(1)如图①所示,连接BF,
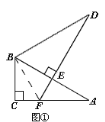
∵BC=BE,
在Rt△BCF和Rt△BEF中
![]()
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF+EF=AC=DE;
(2)如图②所示:
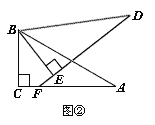
延长DE交AC与点F,连接BF,
在Rt△BCF和Rt△BEF中
![]()
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF+EF=AC=DE;
(3)如图③所示:
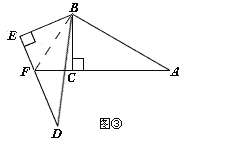
连接BF,
在Rt△BCF和Rt△BEF中
![]()
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF-FC=AC=DE,
∴AF-EF=DE.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】为了解九年级学生的投篮命中率,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.

(1)九年级(1)班的学生人数m= 人,扇形统计图中n= %;
(2)请补全条形统计图;
(3)扇形统计图中“3次”对应的圆心角的度数为 °;
(4)若九年级有学生900人,估计投中次数在2次以上(包括2次)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=2x2+3,下列说法中正确的是 ( )
A. 它的开口方向是向下 B. 当x<-1时,y随x的增大而减小
C. 它的顶点坐标是(2,3) D. 当x=0时,y有最大值是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每千克40元,销售单价与月销售量的关系如下(每千克售价不能高于65元):
![]()
该商品以每千克50元为售价,在此基础上设每千克的售价上涨x元(x为正整数),每个月的销售量为y件.
(1)直接写出y与x的函数关系式,并写出自变量x的取值范围;
(2)设利润为Z元,每千克商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育期末考核“立定跳远”、“800米”、“仰卧起坐”三项,并按3: 5:2的比重算出期末成绩.已知小林这三项的考试成绩分别为80分、90分、100分,则小林的体育期末成绩为分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取1 000名学生的数学成绩,下列说法正确的是( )
A. 2013年昆明市九年级学生是总体 B. 每一名九年级学生是个体
C. 1 000名九年级学生是总体的一个样本 D. 样本容量是1 000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com