
【题目】如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列三个结论:①AP=EF;②△APD一定是等腰三角形;③∠PFE=∠BAP.其中正确结论的序号是( )
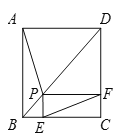
A.①②B.①③C.②③D.①②③
【答案】B
【解析】
连接PC,根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°,然后利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,对应角相等可得∠BAP=∠BCP,再根据矩形的对角线相等可得EF=PC,于是得到结论.
解:如图,连接PC,在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,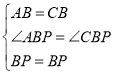 ,
,
∴△ABP≌△CBP(SAS),
∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF是矩形,
∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
故选:B.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表
班级 | 中位数(分) | 众数(分) | 平均数(分) |
一班 | 85 | ||
二班 | 100 | 85 |
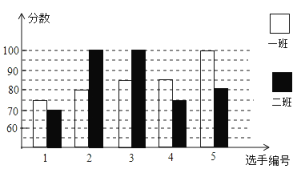
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 的坐标分别为(1,0),(0,2),直线
的坐标分别为(1,0),(0,2),直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
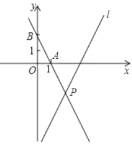
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 在第一象限的直线
在第一象限的直线![]() 上,连接
上,连接![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,点
,点![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,
,![]() 的面积为48.
的面积为48.
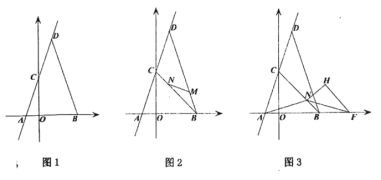
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,连接
上,连接![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,如图3,连接![]() ,点
,点![]() 为
为![]() 轴正半轴上点
轴正半轴上点![]() 右侧一点,点
右侧一点,点![]() 为第一象限内一点,
为第一象限内一点,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,直线
上一点,直线![]() 经过点
经过点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,请你判断四边形
,请你判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
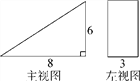
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
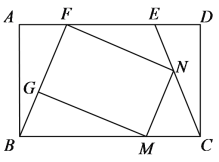
【题目】如图,在矩形ABCD中,点E、F在边AD上,AF=DE,连接BF、CE.
(1)求证:∠CBF=∠BCE;
(2)若点G、M、N在线段BF、BC、CE上,且 FG=MN=CN.求证:MG=NF;
(3)在(2)的条件下,当∠MNC=2∠BMG时,四边形FGMN是什么图形,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,且
,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.
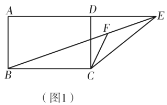
(1)如图1,求![]() 的大小;
的大小;
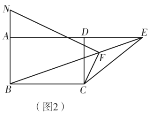
(2)如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;
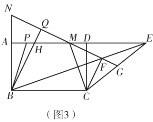
(3)如图3,在(2)的条件下,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,且
,且![]() .延长
.延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的周长与
的周长与![]() 的周长的差为2,求
的周长的差为2,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com